Shadow Terminator in Takua

February 09, 2020 | Tags: Coding, Renderer

I recently implemented two techniques in Takua for solving the harsh shadow terminator problem; I implemented both the Disney Animation solution [Chiang et al. 2019] that we published at SIGGRAPH 2019, and the Sony Imageworks technique [Estevez et al. 2019] published in Ray Tracing Gems. We didn’t show too many comparisons between the two techniques (which I’ll refer to as the Chiang and Estevez approaches, respectively) in our SIGGRAPH 2019 presentation, and we didn’t show comparisons on any actual “real-world” scenes, so I thought I’d do a couple of my own renders using Takua as a bit of a mini-followup and share a handful of practical implementation tips. For a recap of the harsh shadow terminator problem, please see either the Estevez paper or the slides from the Chiang talk, which both do excellent jobs of describing the problem and why it happens in detail. Here’s a small scene that I made for this post, thrown together using some Evermotion assets that I had sitting around:

Figure 1: A simple bedroom scene, rendered in Takua Renderer. This image was rendered using the Chiang 2019 shadow terminator solution.

In this scene, all of the blankets and sheets and pillows on the bed use a fabric material that uses extremely high-frequency, high-resolution normal maps to achieve the fabric-y fiber-y look. Because of these high-frequency normal maps, the bedding is susceptible to the harsh shadow terminator problem. All of the bedding also has diffuse transmission and a very slight amount of high roughness specularity to emulate the look of a sheen lobe, making the material (and therefore this comparison) overall more interesting than just a single diffuse lobe.

Since the overall scene is pretty brightly lit and the bed is lit from all directions either by direct illumination from the window or bounce lighting from inside of the room, the shadow terminator problem is not as apparent in this scene; it’s still there, but it’s much more subtle than in the examples we showed in our talk. Below are some interactive comparisons between renders using Chiang 2019, Estevez 2019, and no shadow terminator fix; drag the slider left and right to compare:

Figure 2: The bedroom scene rendered in Takua Renderer using Chiang 2019 (left) and no harsh shadow terminator fix (right). For a full screen comparison, click here.

Figure 3: The bedroom scene rendered in Takua Renderer using Chiang 2019 (left) and Estevez 2019 (right). For a full screen comparison, click here.

Figure 4: The bedroom scene rendered in Takua Renderer using no normal mapping (left) and normal mapping with no harsh shadow terminator fix (right). For a full screen comparison, click here.

If you would like to compare the 4K renders directly, they are located here: Chiang 2019, Estevez 2019, No Fix, No Normal Mapping. As mentioned above, due to this scene being brightly lit, differences between the two techniques and not having any harsh shadow terminator fix at all will be a bit more subtle. However, differences are still visible, especially in brighter areas of the blanket and white pillows. Note that in this scenario, the difference between Chiang 2019 and Estevez 2019 is fairly small, while the difference between using either shadow terminator fix and not having a fix is more apparent. Also note how both Chiang 2019 and Estevez 2019 produce results that come pretty close to matching the reference image with no normal mapping; this is good, since we would expect fix techniques to match the reference image more closely than not having a fix!

If we remove the bedroom set and put the bed onto more of a studio lighting setup with two area lights and a seamless grey backdrop, we can start seeing more prominent differences between the two techniques and between either technique and no fix. Seeing how everything plays out in this type of a lighting setup is useful, since this is the type of render that one often sees as part of a standard lookdev department’s workflow:

Figure 5: The bed in a studio lighting setup, rendered in Takua Renderer using Chiang 2019 (left) and no harsh shadow terminator fix (right). For a full screen comparison, click here.

Figure 6: The bed in a studio lighting setup, rendered in Takua Renderer using Chiang 2019 (left) and Estevez 2019 (right). For a full screen comparison, click here.

Figure 7: The bed in a studio lighting setup, rendered in Takua Renderer using no normal mapping (left) and normal mapping with no harsh shadow terminator fix (right). For a full screen comparison, click here.

If you would like to compare the 4K renders directly for the studio lighting setup, they are located here: Chiang 2019, Estevez 2019, No Fix, No Normal Mapping. In this setup, we can now see differences between the four images much more clearly. Compared to the no normal mapping reference, the render with no fix produces considerably more darkening on silhouettes, and the harsh sudden transition from bright to shadowed areas is much more apparent. In the render with no fix, the bedding suddenly looks a lot less soft and starts to look a little more like a hard solid surface instead of like fabric.

Chiang 2019 and Estevez 2019 both restore more of the soft fabric look by softening out the harsh shadow terminator areas, but the differences between Chiang 2019 and Estevez 2019 become more apparent and interesting in this setting. Chiang 2019 produces an overall softer look that has shadow terminators that more closely match the reference with no normal mapping, but Chiang 2019 produces a slightly darker look overall compared to Estevez 2019. Estevez 2019 doesn’t match the reference’s shadow terminators quite as closely as Chiang 2019, but manages to preserve more of the overall energy. In Figure 5 in the Chiang 2019 paper, we explain where this difference comes from: for small shading normal deviations, Estevez 2019 produces less shadowing than our method, whereas for larger shading normal deviations, Estevez 2019 produces more shadowing than our method. As a result, Estevez 2019 generally produces a higher contrast look compared to Chiang 2019.

All of these differences are more apparent in a close-up crop of the full 4K render. Here are comparisons of the same studio lighting setup from above, but cropped in; pay close attention to slightly right of center of the image, where the white blanket overhangs the edge of the bed:

Figure 8: Crop of the studio lighting setup render from earlier, using Chiang 2019 (left) and no harsh shadow terminator fix (right). For a larger comparison, click here.

Figure 9: Crop of the studio lighting setup render from earlier, using Chiang 2019 (left) and Estevez 2019 (right). For a larger comparison, click here.

Figure 10: Crop of the studio lighting setup render from earlier, using no normal mapping (left) and normal mapping with no harsh shadow terminator fix (right). For a larger comparison, click here.

Of course, the scenario that makes the harsh shadow terminator problem the most apparent is when there is a single strong light source and we are viewing the scene from an angle from which we can see areas where the light hits surfaces at a glancing angle. These types of lighting setups are often used for checking silhouettes and backlighting and whatnot in modeling and lookdev turntable renders. In the comparisons below, the differences are most noticeable in the folds and on the shadowed sides of all of the bedding:

Figure 11: The bed lit with a single very bright light, rendered in Takua Renderer using Chiang 2019 (left) and no harsh shadow terminator fix (right). For a full screen comparison, click here.

Figure 12: The bed lit with a single very bright light, rendered in Takua Renderer using Chiang 2019 (left) and Estevez 2019 (right). For a full screen comparison, click here.

Figure 13: The bed lit with a single very bright light, rendered in Takua Renderer using no normal mapping (left) and normal mapping with no harsh shadow terminator fix (right). For a full screen comparison, click here.

If you would like to compare the 4K renders directly for the single light source renders, they are located here: Chiang 2019, Estevez 2019, No Fix, No Normal Mapping. With a single light source, the differences between the four images are now very clear, since a single light setup produces strong contrast between the lit and shadowed parts of the image. The harsh shadow terminator problem is especially visible in the folds of the blanket, where we can see one side of the fold fully lit and one side of the fold in shadow (although because the bedding all has diffuse transmission, the harsh shadow terminator is still not as prevalent as it would be for a purely diffuse reflecting surface). Something else that is interesting is how the bedding with no shadow terminator fix overall appears slightly brighter than the bedding with no normal mapping; this is because the shading normals “bend” more light towards the light source. Chiang 2019 restores the overall brightness of the bedding back to something closer to the reference with no normal mapping but softens out more of the fine detail from the normal mapping, while Estevez 2019 preserves more of the fine details but has a brightness level closer to the render with no fix.

Just like in the studio lighting renders, differences become more apparent in close-up crops of the full 4K render. Here are some cropped in comparisons, this time centered more on the top of the bed than on the edge. In these crops, the glancing light angles make the shadow terminators more apparent in the folds of the blankets and such:

Figure 14: Crop of the single light render from earlier, using Chiang 2019 (left) and no harsh shadow terminator fix (right). For a larger comparison, click here.

Figure 15: Crop of the single light render from earlier, using Chiang 2019 (left) and Estevez 2019 (right). For a larger comparison, click here.

Figure 16: Crop of the single light render from earlier, using no normal mapping (left) and normal mapping with no harsh shadow terminator fix (right). For a larger comparison, click here.

In the end, I don’t think either approach is better than the other, and from a physical basis there really isn’t a “right” answer since nothing about shading normals is physical to begin with; I think it’s up to a matter of personal preference and the requirements of the art direction on a given project. Our artists at Walt Disney Animation Studios generally prefer the look of Chiang 2019 because of the lighting setups they usually work with, but I know that other artists prefer the look of Estevez 2019 because they have different requirements to meet.

Fortunately, both Chiang 2019 and Estevez 2019 are both really easy to implement! Both techniques can be implemented in a handful of lines of code, and are easy to apply to any modern physically based shading model. We didn’t actually include source code in our SIGGRAPH talk, mostly because we figured that translating the math from our short paper into code should be very straightforward and thus, including source code that is basically a direct transcription of the math into C++ would almost be insulting to the intelligence of the reader. However, since then, I’ve gotten a surprising number of emails asking for source code, so here’s the math and the corresponding C++ code from my implementation in Takua Renderer. Let G’ be the additional shadow terminator term that we will multiply the Bsdf result with:

\[ G = \min\bigg[1, \frac{\langle\omega_g,\omega_i\rangle}{\langle\omega_s,\omega_i\rangle\langle\omega_g,\omega_s\rangle}\bigg] \]
\[ G' = - G^3 + G^2 + G \]
float calculateChiang2019ShadowTerminatorTerm(const vec3& outputDirection,
                                              const vec3& shadingNormal,
                                              const vec3& geometricNormal) {
    float NDotL = max(0.0f, dot(shadingNormal, outputDirection));
    float NGeomDotL = max(0.0f, dot(geometricNormal, outputDirection));
    float NGeomDotN = max(0.0f, dot(geometricNormal, shadingNormal));
    if (NDotL == 0.0f || NGeomDotL == 0.0f || NGeomDotN == 0.0f) {
        return 0.0f;
    } else {
        float G = NGeomDotL / (NDotL * NGeomDotN);
        if (G <= 1.0f) {
            float smoothTerm = -(G * G * G) + (G * G) + G; // smoothTerm is G' in the math
            return smoothTerm;
        }
    }
    return 1.0f;
}

That’s all there is to it! Source code for Estevez 2019 is provided as part of the Ray Tracing Gems Github repository, but for the sake of completeness, my implementation is included below. My implementation is just the sample implementation streamlined into a single function:

float calculateEstevez2019ShadowTerminatorTerm(const vec3& outputDirection,
                                               const vec3& shadingNormal,
                                               const vec3& geometricNormal) {
    float cos_d = min(abs(dot(geometricNormal, shadingNormal)), 1.0f);
    float tan2_d = (1.0f - cos_d * cos_d) / (cos_d * cos_d);
    float alpha2 = clamp(0.125f * tan2_d, 0.0f, 1.0f);

    float cos_i = max(abs(dot(geometricNormal, outputDirection)), 1e-6f);
    float tan2_i = (1.0f - cos_i * cos_i) / (cos_i * cos_i);
    float spi_shadow_term = 2.0f / (1.0f + sqrt(1.0f + alpha2 * tan2_i));
    return spi_shadow_term;
}

Finally, I have a handful of small implementation notes. First, to apply either Chiang 2019 or Estevez 2019 to your existing physically based shading model, just multiply the additional shadow terminator term with the contribution for each lobe that needs adjusting. Technically speaking G’ is an adjustment to the G shadowing term in a standard microfacet model, but multiplying there versus multiplying with the overall lobe contribution works out to be the same thing. If your Bsdf supports multiple shading normals for different specular lobes, you’ll need to calculate a separate shadow terminator term for each shading normal. Second, note that both Chiang 2019 and Estevez 2019 are described with respect to unidirectional path tracing from the camera. This frame of reference is very important; both techniques work specifically based on the outgoing direction being the direction towards a potential light source, meaning that this technique actually isn’t reciprocal by default. The Estevez 2019 paper found that the shadow terminator term can be made reciprocal by just applying the term to both incoming and outgoing directions, but they also found that this adjustment can make edges too dark. Instead, in order to make both techniques compatible with bidirectional path tracing integrators, I add in a check for whether the incoming or outgoing direction is pointed at a light, and feed the appropriate direction into the shadow terminator function. Doing this check is enough to make my bidirectional renders match my unidirectional ones; intuitively this approach is similar to the check one has to carry out when applying adjoint Bsdf adjustments [Veach 1996] for shading normals and refraction.

That’s pretty much it! If you want the details for how these two techniques are derived and why they work, I strongly encourage reading the Estevez 2019 chapter in Ray Tracing Gems and reading through both the short paper and the presentation slides / notes for the Chiang 2019 SIGGRAPH talk.

References

Matt Jen-Yuan Chiang, Yining Karl Li, and Brent Burley. 2019. Taming the Shadow Terminator. In ACM SIGGRAPH 2019 Talks. Article 71.

Alejandro Conty Estevez, Pascal Lecocq, and Clifford Stein. 2019. A Microfacet-Based Shadowing Function to Solve the Bump Terminator Problem. Ray Tracing Gems (2019), 149-158.

Eric Veach. 1996. Non-Symmetric Scattering in Light Transport Algorithms. In Proc. of Eurographics Workshop on Rendering (Rendering Techniques 1996). 82-91.

Errata

Thanks to Matt Pharr for noticing and pointing out a minor bug in the calculateChiang2019ShadowTerminatorTerm() implementation; the code has been updated with a fix.

RenderMan Art Challenge: Woodville

November 30, 2019 | Tags: Art

Table of Contents

1. Introduction
2. Layout and Framing
3. UVs and Geometry
4. Texturing and Shading
5. Set Dressing the Treehouse
6. Building the Background Forest
7. Lighting and Compositing
8. Conclusion

Introduction

Every once in a while, I make a point of spending some significant personal time working on a personal project that uses tools outside of the stuff I’m used to working on day-to-day (Disney’s Hyperion renderer professionally, Takua Renderer as a hobby). A few times each year, Pixar’s RenderMan group holds an art challenge contest where Pixar provides a un-shaded un-uv’d base model and contestants are responsible for layout, texturing, shading, lighting, additional modeling of supporting elements and surrounding environment, and producing a final image. I thought the most recent RenderMan art challenge, “Woodville”, would make a great excuse for playing with RenderMan 22 for Maya; here’s the final image I came up with:

Figure 1: My entry to Pixar's RenderMan Woodville Art Challenge, titled "Morning Retreat". Base treehouse model is from Pixar; all shading, lighting, additional modeling, and environments are mine. Concept by Vasylina Holod. Model by Alex Shilt © Disney / Pixar - RenderMan "Woodville" Art Challenge.

One big lesson I have learned since entering the rendering world is that there is no such thing as the absolute best overall renderer- there are only renderers that are the best suited for particular workflows, tasks, environments, people, etc. Every in-house renderer is the best renderer in the world for the particular studio that built that renderer, and every commercial renderer is the best renderer in the world for the set of artists that have chosen that renderer as their tool of choice. Another big lesson that I have learned is that even though the Hyperion team at Disney Animation has some of the best rendering engineers in the world, so do all of the other major rendering teams, both commercial and in-house. These lessons are humbling to learn, but also really cool and encouraging if you think about it- these lessons means that for any given problem that arises in the rendering world, as an academic field and as an industry, we get multiple attempts to solve it from many really brilliant minds from a variety of background and a variety of different contexts and environments!

As a result, something I’ve come to strongly believe is that for rendering engineers, there is enormous value in learning to use outside renderers that are not the one we work on day-to-day ourselves. At any given moment, I try to have at least a working familiarity with the latest versions of Pixar’s RenderMan, Solid Angle (Autodesk)’s Arnold, and Chaos Group’s Vray and Corona renderers. All of these renderers are excellent, cutting edge tools, and when new artists join our studio, these are the most common commercial renderers that new artists tend to know how to use. Therefore, knowing how these four renderers work and what vocabulary is associated with them tends to be useful when teaching new artists how to use our in-house renderer, and for providing a common frame of reference when we discuss potential improvements and changes to our in-house renderer. All of the above is the mindset I went into this project with, so this post is meant to be something of a breakdown of what I did, along with some thoughts and observations made along the way. This was a really fun exercise, and I learned a lot!

Layout and Framing

For this art challenge, Pixar supplied a base model without any sort texturing or shading or lighting or anything else. The model is by Alex Shilt, based on a concept by Vasylina Holod. Here is a simple render showing what is provided out of the box:

Figure 2: Base model provided by Pixar, rendered against a white cyclorama background using a basic skydome.

I started with just scouting for some good camera angles. Since I really wanted to focus on high-detail shading for this project, I decided from close to the beginning to pick a close-up camera angle that would allow for showcasing shading detail, at the trade-off of not depicting the entire treehouse. A nice (lazy) bonus is that picking a close-up camera angle meant that I didn’t need to shade the entire treehouse; just the parts in-frame. Instead of scouting using just the GL viewport in Maya, I tried using RenderMan for Maya 22’s IPR mode, which replaces the Maya viewport with a live RenderMan render. This mode wound up being super useful for scouting; being able to interactively play with depth of field settings and see even basic skydome lighting helped a lot in getting a feel for each candidate camera angle. Here are a couple of different white clay test renders I did while trying to find a good camera position and framing:

Figure 3: Candidate camera angle with a close-up focus on the entire top of the treehouse.

Figure 4: Candidate camera angle with a close-up focus on a specific triangular A-frame treehouse cabin.

Figure 5: Candidate camera angle looking down from the top of the treehouse.

Figure 6: Candidate camera angle with a close-up focus on the lower set of treehouse cabins.

I wound up deciding to go with the camera angle and framing in Figure 6 for several reasons. First off, there are just a lot of bits that looked fun to shade, such as the round tower cabin on the left side of the treehouse. Second, I felt that this angle would allow me to limit how expansive of an environment I would need to build around the treehouse. I decided around this point to put the treehouse in a big mountainous mixed coniferous forest, with the reasoning being that tree trunks as large as the ones in the treehouse could only come from huge redwood trees, which only grow in mountainous coniferous forests. With this camera angle, I could make the background environment a single mountainside covered in trees and not have to build a wider vista.

UVs and Geometry

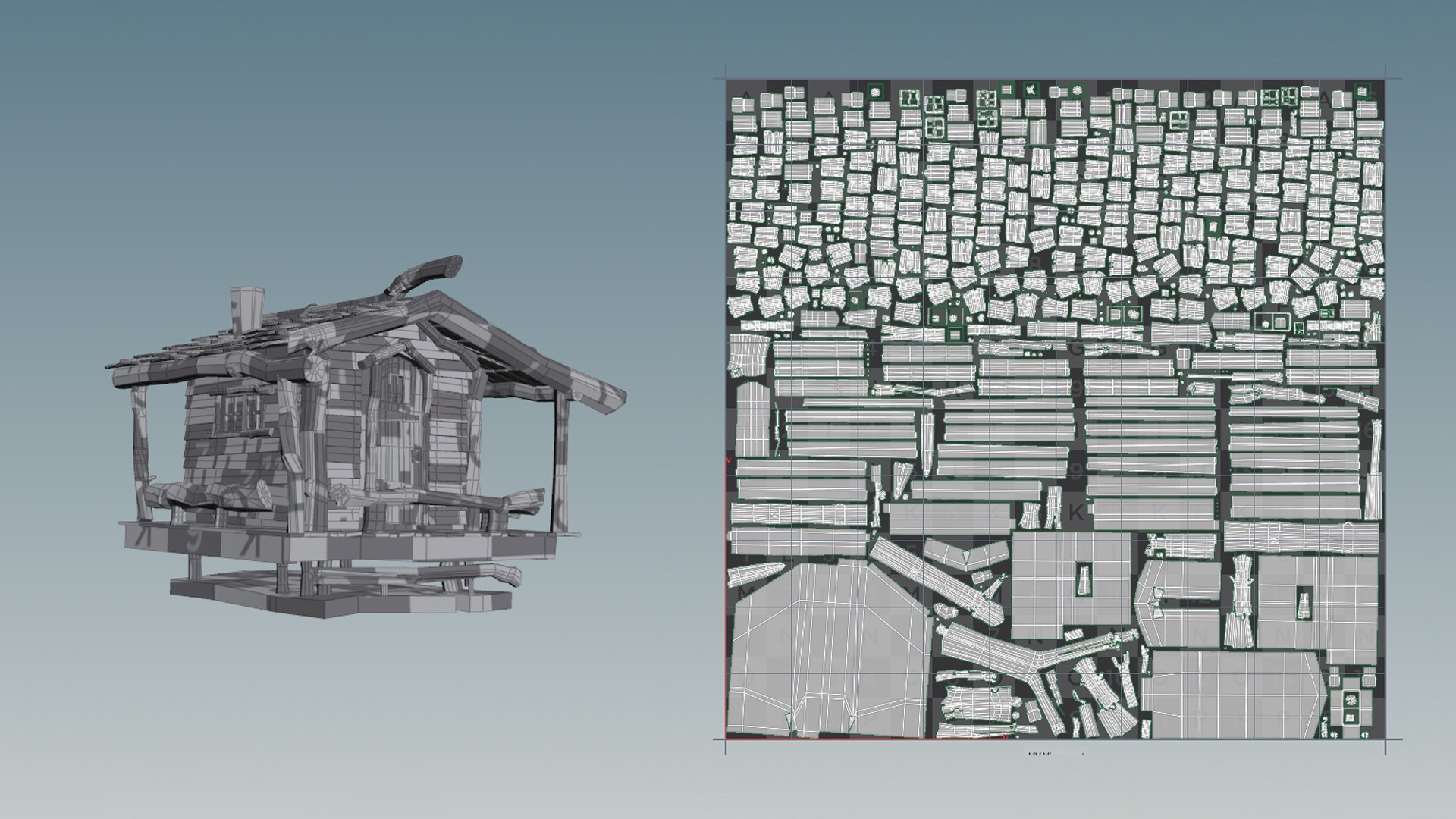
The next step that I took was to try to shade the main tree trunks, since the scale of the tree trunks worried me the most about the entire project. Before I could get to texturing and shading though, I first had to UV-map the tree trunks, and I quickly discovered that before I could even UV-map the tree trunks, I would have to retopologize the meshes themselves, since the tree trunk meshes came with some really messy topology that was basically un-UV-able. I retoplogized the mesh in ZBrush and exported it lower res than the original mesh, and then brought it back into Maya, where I used a shrink-wrap deformer to conform the lower res retopologized mesh back onto the original mesh. The reasoning here was that a lower resolution mesh would be easier to UV unwrap and that displacement later would restore missing detail. Figure 7 shows the wireframe of the original mesh on the left, and the wireframe of my retopologized mesh on the right:

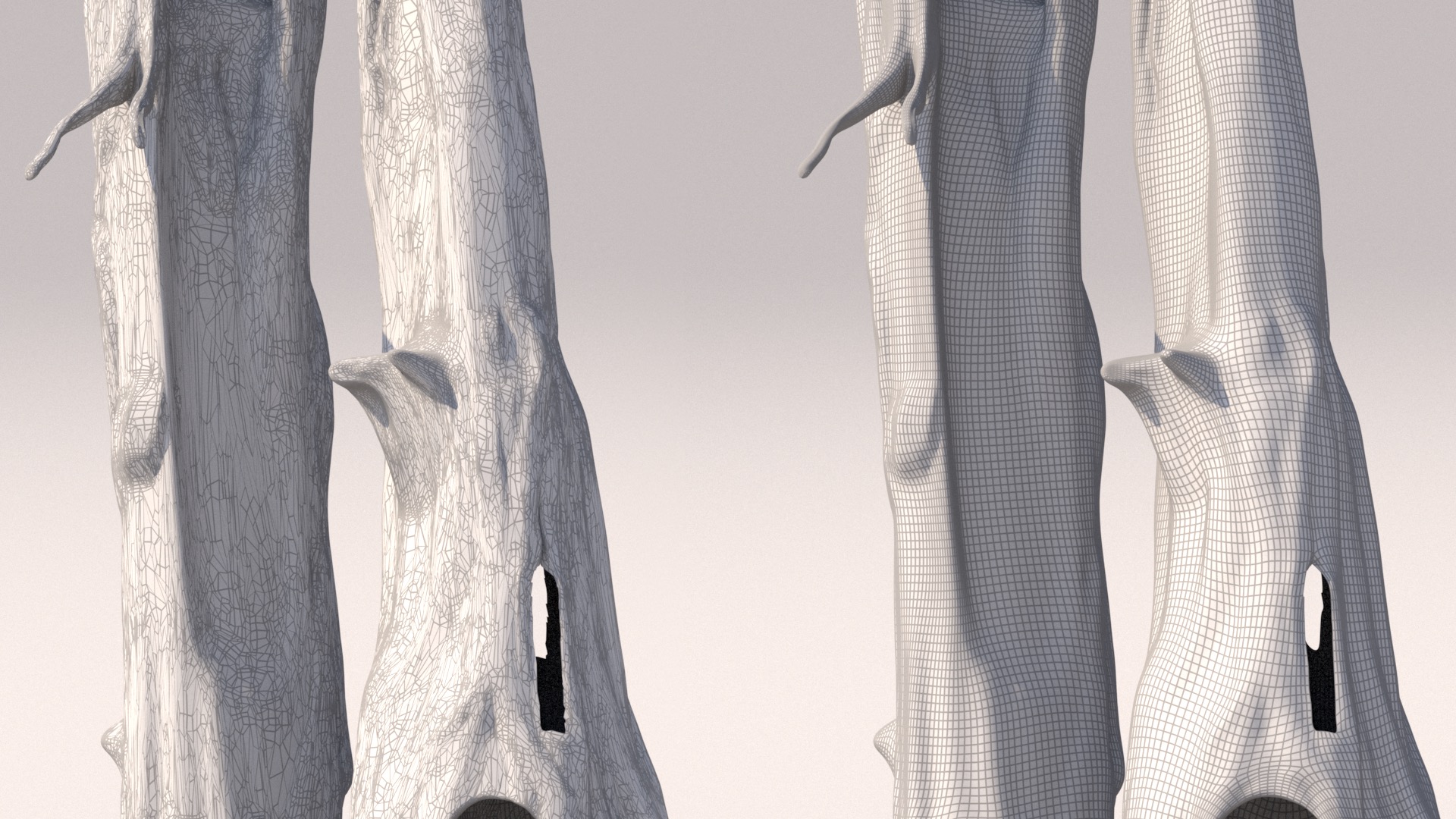
Figure 7: Original mesh wireframe on the left, my retopologized version on the right.

In previous projects, I’ve found a lot of success in using Wenzel Jakob’s Instance Meshes application to retopologize messy geometry, but this time around I used ZBrush’s ZRemesher tool since I wanted as perfect a quad grid as possible (at the expense of losing some mesh fidelity) to make UV unwrapping easier. I UV-unwrapped the remeshed tree trunks by hand; the general approach I took was to slice the tree trunks into a series of stacked cylinders and then unroll each cylinder into as rectangular of a UV shell as I could. For texturing, I started with some photographs of redwood bark I found online, turned them greyscale in Photoshop and adjusted levels and contrast to produce height maps, and then took the height maps and source photographs into Substance Designer, where I made the maps tile seamlessly and also generated normal maps. I then took the tileable textures into Substance Painter and painted the tree trunks using a combination of triplanar projections and manual painting. At this point, I had also blocked in a temporary forest in the background made from just instancing two or three tree models all over the place, which I found useful for being able to help get a sense of how the shading on the treehouse was working in context:

Figure 8: In-progress test render with shaded tree trunks and temporary background forest blocked in.

Next up, I worked on getting base shading done for the cabins and various bits and bobs on the treehouse. The general approach I took for the entire treehouse was to do base texturing and shading in Substance Painter, and then add wear and tear, aging, and moss in RenderMan through procedural PxrLayerSurface layers driven by a combination of procedural PxrRoundCube and PxrDirt nodes and hand-painted dirt and wear masks. First though, I had to UV-unwrap all of the cabins and stuff. I tried using Houdini’s Auto UV SOP that comes with Houdini’s Game Tools package… the result (for an example, see Figure 9) was really surprisingly good! In most cases I still had to do a lot of manual cleanup work, such as re-stitching some UV shells together and re-laying-out all of the shells, but the output from Houdini’s Auto UV SOP provided a solid starting point. For each cabin, I grouped surfaces that were going to have a similar material into a single UDIM tile, and sometimes I split similar materials across multiple UDIM tiles if I wanted more resolution. This entire process was… not really fun… it took a lot of time and was basically just busy-work. I vastly prefer being able to paint Ptex instead of having to UV-unwrap and lay out UDIM tiles, but since I was using Substance Painter, Ptex wasn’t an option on this project.

Figure 9: Example of one of the cabins run through Houdini's Auto UV SOP. The cabin is on the left; the output UVs are on the right.

Texturing in Substance Painter and Shading

In Substance Painter, the general workflow I used was to start with multiple triplanar projections of (heavily edited) Quixel Megascans surfaces masked and oriented to different sections of a surface, and then paint on top. Through this process, I was able to get bark to flow with the curves of each log and whatnot. Then, in RenderMan for Maya, I took all of the textures from Substance Painter and used them to drive the base layer of a PxrLayeredSurface shader. All of the textures were painted to be basically greyscale or highly desaturated, and then in Maya I used PxrColorCorrect and PxrVary nodes to add in color. This way, I was able to iteratively play with and dial in colors in RenderMan’s IPR mode without having to roundtrip back to Substance Painter too much. Since the camera in my frame is relatively close to the treehouse, having lots of detail was really important. I put high-res displacement and normal maps on almost everything, which I found helpful for getting that extra detail in. I found that setting micropolygon length to be greater than 1 polygon per pixel was useful for getting extra detail in with displacement, at the cost of a bit more memory usage (which was perfectly tolerable in my case).

One of the unfortunate things about how I chose to UV-unwrap the tree trunks is that UV seams cut across parts of the tree trunks that are visible to the camera; as a result, if you zoom into the final 4K renders, you can see tiny line artifacts in the displacement where UV seams meet. These artifacts arise from displacement values not interpolating smoothly across UV seams when texture filtering is in play; this problem can sometimes be avoided by very carefully hiding UV seams, but sometimes there is no way. The problem in my case is somewhat reduced by expanding displacement values beyond the boundaries of each UV shell in the displacement textures (most applications like Substance Painter can do this natively), but again, this doesn’t completely solve the problem, since expanding values beyond boundaries can only go so far until you run into another nearby UV shell and since texture filtering widths can be variable. This problem is one of the major reasons why we use Ptex so heavily at Disney Animation; Ptex’s robust cross-face filtering functionality sidesteps this problem entirely. I really wish Substance Painter could output Ptex!

For dialing in the colors of the base wood shaders, I created versions of the wood shader base color textures that looked like newer wood and older sun-bleached wood, and then I used a PxrBlend node in each wood shader to blend between the newer and older looking wood, along with procedural wear to make sure that the blend wasn’t totally uniform. Across all of the various wood shaders in the scene, I tied all of the blend values to a single PxrToFloat node, so that I could control how aged all wood across the entire scene looks with a single value. For adding moss to everything, I used a PxrRoundCube triplanar to set up a base mask for where moss should go. The triplanar mask was set up so that moss appears heavily on the underside of objects, less on the sides, and not at all on top. The reasoning for making moss appear on undersides is because in the type of conifer forest I set my scene in, moss tends to grow where moisture and shade are available, which tends to be on the underside of things. The moss itself was also driven by a triplanar projection and was combined into each wood shader as a layer in PxrLayerSurface. I also did some additional manual mask painting in Substance Painter to get moss into some more crevices and corners and stuff on all of the wooden sidings and the wooden doors and whatnot. Finally, the overall amount of moss across all of the cabins is modulated by another single PxrToFloat node, allowing me to control the overall amount of moss using another single value. Figure 10 shows how I could vary the age of the wood on the cabins, along with the amount of moss.

Figure 10: Example of age and moss controllability on one of the cabins. The top row shows, going from left to right, 0% aged, 50% aged, and 100% aged. The bottom row shows, going from left to right, 0% moss, 50% moss, and 100% moss. The final values used were close to 60% for both age and moss.

The spiral staircase initially made me really worried; I originally thought I was going to have to UV unwrap the whole thing, and stuff like the railings are really not easy to unwrap. But then, after a bit of thinking, I realized that the spiral staircase is likely a fire escape staircase, and so it could be wrought iron or something. Going with a wrought iron look allowed me to handle the staircase mostly procedurally, which saved a lot of time. Going along with the idea of the spiral staircase being a fire escape, I figured that the actual main way to access all of the different cabins in the treehouse must be through staircases internal to the tree trunks. This idea informed how I handled that long skinny window above the front door; I figured it must be a window into a stairwell. So, I put a simple box inside the tree behind that window, with a light at the top. That way, a hint of inner space would be visible through the window:

Figure 11: Simple box inside the tree behind the lower window, to give a hint of inner space.

In addition to shading everything, I also had to make some modifications to the provided treehouse geometry. I that in the provided model, the satellite dish floats above its support pole without any actual connecting geometry, so I modeled a little connecting bit for the satellite dish. Also, I thought it would be fun to put some furniture in the round cabin, so I decided to make the walls into plate glass. Once I made the walls into plate glass, I realized that I needed to make a plausible interior for the round cabin. Since the only way into the round cabin must be through a staircase in the main tree trunk, I modeled a new door in the back of the round cabin. With everything shaded and the geometric modifications in place, here is how everything looked at this point:

Figure 12: In-progress test render with initial fully shaded treehouse, along with geoemtric modifications. Click for 4K version.

Set Dressing the Treehouse

The next major step was adding some story elements. I wanted the treehouse to feel lived in, like the treehouse is just somebody’s house (a very unusual house, but a house nonetheless). To help convey that feeling, my plan was to rely heavily on set dressing to hint at the people living here. So the goal was to add stuff like patio furniture, potted plants, laundry hanging on lines, furniture visible through windows, the various bits and bobs of life, etc.

I started by adding a nice armchair and a lamp to the round tower thing. Of course the chair is an Eames Lounge Chair, and to match, the lamp is a modern style tripod floor lamp type thing. I went with a chair and a lamp because I think that round tower would be a lovely place to sit and read and look out the window at the surrounding nature. I thought it would be kind of fun to make all of the furniture kind of modern and stylish, but have all of the modern furniture be inside of a more whimsical exterior. Next, I extended the front porch part of the main cabin, so that I could have some room to place furniture and props and stuff. Of course any good front porch should have some nice patio furniture, so I added some chairs and a table. I also put in a hanging round swing chair type thing with a bit poofy blue cushion; this entire area should be a fun place to sit around and talk in. Since the entire treehouse sits on the edge of a pond, I figured that maybe the people living here like to sit out on the front porch, relax, shoot the breeze, and fish from the pond. Since my scene is set in the morning, I figured maybe it’s late in the morning and they’ve set up some fishing lines to catch some fish for dinner later. To help sell the idea that it’s a lazy fishing morning, I added a fishing hat on one of the chairs and put a pitcher of ice tea and some glasses on the table. I also added a clothesline with some hanging drying laundry, along with a bunch of potted and hanging plants, just to add a bit more of that lived-in feel. For the plants and several of the furniture pieces that I knew I would want to tweak later, I built in controls to their shading graphs using PxrColorCorrect nodes to allow me to adjust hue and saturation later. Many of the furniture, plant and prop models are highly modified, kitbashed, re-textured versions of assets from Evermotion and CGAxis, although some of them (notably the Eames Lounge Chair) are entirely my own.

Figure 13: In-progress test render closeup crop of the lower main cabin, with furniture and plants and props.

Figure 14: In-progress test render closeup crop of the glass round cabin and the upper smaller cabin, with furniture and plants and props.

Building the Background Forest

The last step before final lighting was to build a more proper background forest, as a replacement for the temporary forest I had used up until this point for blocking purposes. For this step, I relied heavily on Maya’s MASH toolset, which I found to provide a great combination of power and ease-of-use; for use cases involving tons of instanced geometry, I certainly found it much easier than Maya’s older Xgen toolset. MASH felt a lot more native to Maya, as opposed to Xgen, which requires a bunch of specific external file paths and file formats and whatnot. I started with just getting some kind of reasonable base texturing down onto the groundplane. In all of the in-progress renders up until this point, the ground plane was just white… you can actually tell if you look closely enough! I eventually got to a place I was happy with using a bunch of different PxrRoundCubes with various rotations, all blended on top of each other using various noise projections. I also threw in some rocks from Quixel Megascans, just to add a bit of variety. I then laid down some low-level ground vegetation, which was meant to peek through the larger trees in various areas. The base vegetation was made up of various ferns, shrubs, and small sapling-ish young conifers placed using Maya’s MASH Placer node:

Figure 15: In-progress test render of the forest floor and under-canopy vegetation.

In the old temporary background forest, the entire forest is made up of only three different types of trees, and it really shows; there was a distinct lack of color variation or tree diversity. So, for the new forest, I decided to use a lot more types of trees. Here is a rough lineup (not necessarily to scale with each other) of how all of the new tree species looked:

Figure 16: Test render of a lineup of the trees used in the final forest.

For the main forest, I hand-placed trees onto the mountain slope as instanced. One cool thing I built in to the forest was PxrColorCorrect nodes in all of the tree shading graphs, with all controls wired up to single master controls for hue/saturation/value so that I could shift the entire forest’s colors easily if necessary. This tool proved to be very useful for tuning the overall vegetation colors later while still maintaining a good amount of variation. I also intentionally left gaps in the forest around the rock formations to give some additional visual variety. Building up the entire under-layer of shrubs and saplings and stuff also paid off, since a lot of that stuff wound up peeking through various gaps between the larger trees:

Figure 17: In-progress test render of the background forest.

The last step for the main forest was adding some mist and fog, which is common in Pacific Northwest type mountainous conifer forests in the morning. I didn’t have extensive experience working with volumes in RenderMan before this, so there was definitely something of a learning curve for me, but overall it wasn’t too hard to learn! I made the mist by just having a Maya Volume Noise node plug into the density field of a PxrVolume; this isn’t anything fancy, but it provided a great start for the mist/fog:

Figure 18: In-progress test render of the background forest with an initial version of mist and fog.

Lighting and Compositing

At this point, I think the entire image together was starting to look pretty good, although, without any final shot lighting, the overall vibe felt more like a spread out of an issue of National Geographic than a more cinematic still out of a film. Normally my instinct is to go with a more naturalistic look, but since part of the objective for this project was to learn to use RenderMan’s lighting toolset for more cinematic applications, I wanted to push the overall look of the image beyond this point:

Figure 19: In-progress test render with everything together, before final shot lighting.

From this point onwards, following a tutorial made by Jeremy Heintz, I broke out the volumetric mist/fog into a separate layer and render pass in Maya, which allowed for adjusting the mist/fog in comp without having to re-render the entire scene. This strategy proved to be immensely useful and a huge time saver in final lighting. Before starting final lighting, I made a handful of small tweaks, which included reworking the moss on the front cabin’s lower support frame to get rid of some visible repetition, tweaking and adding dirt on all of the windows, and dialing in saturation and hue on the clothesline and potted plants a bit more. I also changed the staircase to have aged wooden steps instead of all black cast iron, which helped blend the staircase into the overall image a bit more, and finally added some dead trees in the background forest. Finally, in a last-minute change, I wound up upgrading a lot of the moss on the main tree trunk and on select parts of the cabins to use instanced geometry instead of just being a shading effect. The geometric moss used atlases from Quixel Megascans, bunched into little moss patches, and then hand-scattered using the Maya MASH Placer tool. Upgrading to geometric moss overall provided only a subtle change to the overall image, but I think helped enormously in selling some of the realism and detail; I find it interesting how small visual details like this often can have an out-sized impact on selling an overall image.

For final lighting, I added an additional uniform atmospheric haze pass to help visually separate the main treehouse from the background forest a bit more. I also added a spotlight fog pass to provide some subtle godrays; the spotlight is a standard PxrRectLight oriented to match the angle of the sun. The PxrRectLight also has the cone modified enabled to provide the spot effect, and also has a PxrCookieLightFilter applied with a bit of a cucoloris pattern applied to provide the breakup effect that godrays shining through a forest canopy should have. To provide a stronger key light, I rotated the skydome until I found something I was happy with, and then I split out the sun from the skydome into separate passes. I split out the sun by painting the sun out of the skydome texture and then creating a PxrDistantLight with an exposure, color, and angle matched to what the sun had been in the skydome. Splitting out the sun then allowed me to increase the size of the sun (and decrease the exposure correspondingly to maintain overall the same brightness), which helped soften some otherwise pretty harsh sharp shadows. I also used a good number of PxrRodLightFilters to help take down highlights in some areas, lighten shadows in others, and provide overall light shaping to areas like the right hand side of the right tree trunk. I’ve conceptually known why artists like rods for some time now (especially since rods are heavily used feature in Hyperion at my day job at Disney Animation), but I think this project helped me really understand at a more hands-on level why rods are so great for hitting specific art direction.

After much iteration, here is the final set of render passes I wound up with going into final compositing:

Figure 19: Final render, sun (key) pass. Click for 4K version.

Figure 20: Final render, sky (fill) pass. Click for 4K version.

Figure 21: Final render, practical lights pass. Click for 4K version.

Figure 22: Final render, mist/fog pass. Click for 4K version.

Figure 23: Final render, atmospheric pass. Click for 4K version.

Figure 24: Final render, spotlight pass. Click for 4K version.

In final compositing, since I had everything broken out into separate passes, I was able to quickly make a number of adjustments that otherwise would have been much slower to iterate on if I had done them in-render. I tinted the sun pass to be warmer (which is equivalent to changing the sun color in-render and re-rendering) and tweaked the exposures of the sun pass up and some of the volumetric passes down to balance out the overall image. I also applied a color tint to the mist/fog pass to be cooler, which would have been very slow to experiment with if I had changed the actual fog color in-render. I did all of the compositing in Photoshop, since I don’t have a Nuke license at home. Not having a node-based compositing workflow was annoying, so next time I’ll probably try to learn DaVinci Resolve Fusion (which I hear is pretty good).

For color grading, I mostly just fiddled around in Lightroom. I also added in a small amount of bloom by just duplicating the sun pass, clipping it to only really bright highlight values by adjusting levels in Photoshop, applying a Gaussian blur, exposing down, and adding back over the final comp. Finally, I adjusted the gamma by 0.8 and exposed up by half a stop to give some additional contrast and saturation, which helped everything pop a bit more and feel a bit more moody and warm. Figure 25 shows what all of the lighting, comp, and color grading looks like applied to a 50% grey clay shaded version of the scene, and if you don’t want to scroll all the way back to the top of this post to see the final image, I’ve included it again as Figure 26.

Figure 25: Final lighting, comp, and color grading applied to a 50% grey clay shaded version. Click for 4K version.

Figure 26: Final image. Click for 4K version.

Conclusion

Overall, I had a lot of fun on this project, and I learned an enormous amount! This project was probably the most complex and difficult art project I’ve ever done. I think working on this project has shed a lot of light for me on why artists like certain workflows, which is an incredibly important set of insights for my day job as a rendering engineer. I won’t grumble as much about having to support rods in production rendering now!

Here is a neat progression video I put together from all of the test and in-progress renders that I saved throughout this entire project:

I owe several people an enormous debt of thanks on this project. My wife, Harmony Li, deserves all of my gratitude for her patience with me during this project, and also for being my art director and overall sanity checker. My coworker at Disney Animation, lighting supervisor Jennifer Yu, gave me a lot of valuable critiques, advice, and suggestions, and acted as my lighting director during the final lighting and compositing stage. Leif Pederson from Pixar’s RenderMan group provided a lot of useful tips and advice on the RenderMan contest forum as well.

Finally, my final image somehow managed to score an honorable mention in Pixar’s Art Challenge Final Results, which was a big, unexpected, pleasant surprise, especially given how amazing all of the other entries in the contest are! Since the main purpose of this project for me was as a learning exercise, doing well in the actual contest was a nice bonus, and kind of makes me think I’ll likely give the next RenderMan Art Challenge a shot too with a more serious focus on trying to put up a good showing. If you’d like to see more about my contest entry, check out the work-in-progress thread I kept up in Pixar’s Art Challenge forum; some of the text for this post was adapted from updates I made in my forum thread.

Frozen 2

November 14, 2019 | Tags: Films

The 2019 film from Walt Disney Animation Studios is, of course, Frozen 2, which really does not need any additional introduction. Instead, here is a brief personal anecdote. I remember seeing the first Frozen in theaters the day it came out, and at some point halfway through the movie, it dawned on me that what was unfolding on the screen was really something special. By the end of the first Frozen, I was convinced that I had to somehow get myself a job at Disney Animation some day. Six years later, here we are, with Frozen 2’s release imminent, and here I am at Disney Animation. Frozen 2 is my fourth credit at Disney Animation, but somehow seeing my name in the credits at the wrap party for this film was even more surreal than seeing my name in the credits on my first film. Working with everyone on Frozen 2 was an enormous privilege and thrill; I’m incredibly proud of the work we have done on this film!

Under team lead Dan Teece’s leadership, for Frozen 2 we pushed Disney’s Hyperion Renderer the hardest and furthest yet to date, and I think the result really shows in the final film. Frozen 2 is stunningly beautiful to look at it; seeing it for the first time in its completed form was a humbling experience, since there were many moments where I realized I honestly had no idea how our artists had managed to push the renderer as far as they did. During the production of Frozen 2, we also welcomed three superstar rendering engineers to the rendering team: Mark Lee, Joe Schutte, and Wei-Feng Wayne Huang; their contributions to our team and to Frozen 2 simply cannot be overstated!

On Frozen 2, I got to play a part on several fun and interesting initiatives! Hyperion’s modern volume rendering system saw a number of major improvements and advancements for Frozen 2, mostly centered around rendering optically thin volumes. Hyperion’s modern volume rendering system is based on null-collision tracking theory [Kutz et al. 2017], which is exceptionally well suited for dense volumes dominated by high-order scattering (such as clouds and snow). However, as anyone with experience developing a volume rendering system knows, optically thin volumes (such as mist and fog) are a major weak point for null-collision techniques . Wayne was responsible for a number of major advancements that allowed us to efficiently render mist and fog on Frozen 2 using the modern volume rendering system, and Wayne was kind enough to allow me to play something of an advisory / consulting role on that project. Also, Frozen 2 is the first feature film on which we’ve deployed Hyperion’s path guiding implementation into production; this project was the result of some very tight collaboration between Disney Animation and Disney Research Studios. Last summer, I worked with Peter Kutz, our summer intern Laura Lediaev, and with Thomas Müller from ETH Zürich / Disney Research Studios to prototype an implementation of Practical Path Guiding [Müller et al. 2017] in Hyperion. Joe Schutte then took on the massive task (as one of his first tasks on the team, no less!) of turning the prototype into a production-quality feature, and Joe worked with Thomas to develop a number of improvements to the original paper [Müller 2019]. Finally, I worked on some lighting / shading improvements for Frozen 2, which included developing a new spot light implementation for theatrical lighting, and, with Matt Chiang and Brent Burley, a solution to the long-standing normal / bump mapped shadow terminator problem [Chiang et al. 2019]. We also benefited from more improvements in our denoising tech [Dahlberg et al. 2019] which arose as a joint effort between our own David Adler, ILM, Pixar and the Disney Research Studios rendering team.

I think Frozen projects provide an interesting window into how far rendering has progressed at Disney Animation over the past six years. We’ve basically had some Frozen project going on every few years, and each Frozen project upon completion has represented the most cutting edge rendering capabilities we’ve had at the time. The original Frozen in 2013 was the studio’s last project rendered using Renderman, and also the studio’s last project to not use path tracing. Frozen Fever in 2015, by contrast, was one of the first projects (alongside Big Hero 6) to use Hyperion and full path traced global illumination. The jump in visual quality between Frozen and Frozen Fever was enormous, especially considering that they were released only a year and a half apart. Olaf’s Frozen Adventure, which I’ve written about before, served as the testbed for a number of enormous changes and advancements that were made to Hyperion in preparation for Ralph Breaks the Internet. Frozen 2 represents the full extent of what Hyperion can do today, now that Hyperion is a production-hardened, mature renderer backed by a team that is now very experienced. The original Frozen looked decent when it first came out, but since it was the last non-path-traced film we made, it looked dated visually just a few years later. Comparing the original Frozen with Frozen 2 is like night and day; I’m very confident that Frozen 2 will still look visually stunning and hold up well long into the future. A great example is in all of the clothing in Frozen 2; when watching the film, take a close look at all of the embroidery on all of the garments. In the original Frozen, a lot of the embroidery work is displacement mapped or even just normal mapped, but in Frozen 2, all of the embroidery is painstakingly constructed from actual geometric curves [Liu et al. 2020], and as a result every bit of embroidery is rendered in incredible detail!

One particular thing in Frozen 2 that makes me especially happy is how all of the water looks in the film, and especially how the water looks in the dark seas sequence. On Moana, we really struggled with getting whitewater and foam to look appropriately bright and white. Since that bright white effect comes from high-order scattering in volumes and at the time we were still using our old volume rendering system that couldn’t handle high-order scattering well, the artists on Moana wound up having to rely on a lot of ingenious trickery to get whitewater and foam to look just okay. I think Moana is a staggeringly beautiful film, but if you know where to look, you may be able to tell that the foam looks just a tad bit off. On Frozen 2, however, we were able to do high-order scattering, and as a result, all of the whitewater and foam in the dark seas sequence looks just absolutely amazing. No spoilers, but all I’ll say is that there’s another part in the movie that isn’t in any trailer where my jaw was just on the floor in terms of water rendering; you’ll know it when you see it. A similar effect has been done before in a previous CG Disney Animation movie, but the effect in Frozen 2 is on a far grander, far more impressive, far more amazing scale [Tollec et al. 2020].

In addition to the rendering tech advancements we made on Frozen 2, there are a bunch of other cool technical initiatives that I’d recommend reading about! Each of our films has its own distinct world and look, and the style requirements on Frozen 2 often required really cool close collaborations between the lighting and look departments and the rendering team; the “Show Yourself” sequence near the end of the film was a great example of the amazing work these collaborations can produce [Sathe et al. 2020]. Frozen 2 had a lot of characters that were actually complex effects, such as the Wind Spirit [Black et al. 2020] and the Nokk water horse [Hutchins et al. 2020]; these characters required tight collaborations between a whole swath of departments ranging from animation to simulation to look to effects to lighting. Even the forest setting of the film required new tech advancements; we’ve made plenty of forests before, but integrating huge-scale effects into the forest resulted in some cool new workflows and techniques [Joseph et al. 2020].

To give a sense of just how gorgeous Frozen 2 looks, below are some stills from the movie, in no particular order, 100% rendered using Hyperion. If you love seeing cutting edge rendering in action, I strongly encourage going to see Frozen 2 on the biggest screen you can find! The film has wonderful songs, a fantastic story, and developed, complex, funny characters, and of course there is not a single frame in the movie that isn’t stunningly beautiful.

Here is the part of the credits with Disney Animation’s rendering team, kindly provided by Disney! I always encourage sitting through the credits for movies, since everyone in the credits put so much hard work and passion into what you see onscreen, but I especially recommend it for Frozen 2 since there’s also a great post-credits scene.

All images in this post are courtesy of and the property of Walt Disney Animation Studios.

References

Cameron Black, Trent Correy, and Benjamin Fiske. 2020. Frozen 2: Creating the Wind Spirit. In ACM SIGGRAPH 2020 Talks. Article 22.

Matt Jen-Yuan Chiang, Yining Karl Li, and Brent Burley. 2019. Taming the Shadow Terminator. In ACM SIGGRAPH 2019 Talks. Article 71.

Henrik Dahlberg, David Adler, and Jeremy Newlin. 2019. Machine-Learning Denoising in Feature Film Production. In ACM SIGGRAPH 2019 Talks. Article 21.

David Hutchins, Cameron Black, Marc Bryant, Richard Lehmann, and Svetla Radivoeva. 2020. “Frozen 2”: Creating the Water Horse . In ACM SIGGRAPH 2020 Talks. Article 23.

Norman Moses Joseph, Vijoy Gaddipati, Benjamin Fiske, Marie Tollec, and Tad Miller. 2020. Frozen 2: Effects Vegetation Pipeline. In ACM SIGGRAPH 2020 Talks. Article 7.

Peter Kutz, Ralf Habel, Yining Karl Li, and Jan Novák. 2017. Spectral and Decomposition Tracking for Rendering Heterogeneous Volumes. ACM Transactions on Graphics (Proc. of SIGGRAPH) 36, 4 (Aug. 2017), Article 111.

Ying Liu, Jared Wright, and Alexander Alvarado. 2020. Making Beautiful Embroidery for “Frozen 2”. In ACM SIGGRAPH 2020 Talks. Article 73.

Thomas Müller. 2019. Practical Path Guiding in Production. In ACM SIGGRAPH 2019 Course Notes: Path Guiding in Production. 37-50.

Thomas Müller, Markus Gross, and Jan Novák. 2017. Practical Path Guiding for Efficient Light-Transport Simulation. Computer Graphics Forum (Proc. of Eurographics Symposium on Rendering) 36, 4 (Jun. 2017), 91-100.

Amol Sathe, Lance Summers, Matt Jen-Yuan Chiang, and James Newland. 2020. The Look and Lighting of “Show Yourself” in “Frozen 2”. In ACM SIGGRAPH 2020 Talks. Article 71.

Marie Tollec, Sean Jenkins, Lance Summers, and Charles Cunningham-Scott. 2020. Deconstructing Destruction: Making and Breaking of ”Frozen 2”’s Dam. In ACM SIGGRAPH 2020 Talks. Article 24.

SIGGRAPH 2019 Talk- Taming the Shadow Terminator

August 01, 2019 | Tags: Hyperion, Shading, SIGGRAPH

This year at SIGGRAPH 2019, Matt Jen-Yuan Chiang, Brent Burley, and I had a talk that presents a technique for smoothing out the harsh shadow terminator problem that often arises when high-frequency bump or normal mapping is used in ray tracing. We developed this technique as part general development on Disney’s Hyperion Renderer for the production of Frozen 2. This work is mostly Matt’s; Matt was very kind in allowing me to help out and play a small role on this project.

This work is contemporaneous with the recent work on the same shadow terminator problem that was carried out and published by Estevez et al. from Sony Pictures Imageworks and published in Ray Tracing Gems. We actually found out about the Estevez et al. technique at almost exactly the same time that we submitted our SIGGRAPH talk, which proved to be very fortunate, since after our talk was accepted, we were than able to update our short paper with additional comparisons between Estevez et al. and our technique. I think this is a great example of how having multiple rendering teams in the field tackling similar problems and sharing results provides a huge benefit to the field as a whole- we now have two different, really good solutions to what used to be a big shading problem!

A higher-res version of Figure 1 from the paper: (left) <a href="https://blog.yiningkarlli.com/content/images/2019/Aug/header_shadingnormals.png">shading normals</a> exhibiting the harsh shadow terminator problem, (center) <a href="https://blog.yiningkarlli.com/content/images/2019/Aug/header_chiang.png">our technique</a>, and (right) <a href="https://blog.yiningkarlli.com/content/images/2019/Aug/header_estevez.png">Estevez et al.'s technique</a>.

Here is the paper abstract:

A longstanding problem with the use of shading normals is the discontinuity introduced into the cosine falloff where part of the hemisphere around the shading normal falls below the geometric surface. Our solution is to add a geometrically derived shadowing function that adds minimal additional shadowing while falling smoothly to zero at the terminator. Our shadowing function is simple, robust, efficient and production proven.

The paper and related materials can be found at:

Matt Chiang presented the paper at SIGGRAPH 2019 in Log Angeles as part of the “Lucy in the Sky with Diamonds - Processing Visuals” Talks session. A pdf version of the presentation slides, along with presenter notes, are available on my project page for the paper. I’d also recommend getting the author’s version of the short paper instead of the official version as well, since the author’s version includes some typo fixes made after the official version was published.

Work on this project started early in the production of Frozen 2, when our look artists started to develop the shading of the dresses and costumes in Frozen 2. Because intricate woven fabrics and patterns are an important part of the Scandinavian culture that Frozen 2 is inspired by, the shading in Frozen 2 pushed high-resolution high-frequency displacing and normal mapping further than we ever had before with Hyperion in order to make convincing looking textiles. Because of how high-frequency the normal mapping was pushed, the bump/normal mapped shadow terminator problem became worse and worse and proved to be a major pain point for our look and lighting artists. In the past, our look and lighting artists have worked around shadow terminator issues using a combination of techniques, such as falling back to full displacement, or using larger area lights to try to soften the shadow terminator. However, these techniques can be problematic when they are in conflict with art direction, and force artists to think about an additional technical dimension when they otherwise would rather be focused on the artistry.

Our search for a solution began with Peter Kutz looking at “Microfacet-based Normal Mapping for Robust Monte Carlo Path Tracing” by Schüssler et al., which focused on addressing energy loss when rendering shading normals. The Schüssler et al. 2017 technique solved the energy loss problem by constructing a microfacet surface comprised of two facets per shading point, instead the the usual one. The secondary facet is used to account for things like inter-reflections between the primary and secondary facets. However, the Schüssler et al. 2017 technique wound up not solving the shadow terminator problems we were facing; using their shadowing function produced a look that was too flat.

Matt Chiang then realized that the secondary microfacet approach could be used to solve the shadow terminator problem using a different secondary microfacet configuration; instead of using a vertical second facet as in Schüssler, Matt made the secondary facet perpendicular to the shading normal. By making the secondary facet perpendicular, as a light source slowly moves towards the grazing angle relative to the microfacet surface, peak brightness is maintained when the light is parallel to the shading normal, while additional shadowing is introduced beyond the parallel angle. This solution worked extremely well, and is the technique presented in our talk / short paper.

The final piece of the puzzle was addressing a visual discontinuity produced by Matt’s technique when the light direction reaches and moves beyond the shading normal. Instead of falling smoothly to zero, the shape of the shadow terminator undergoes a hard shift from a cosing fall-off formed by the dot product of the shading normal and light direction to a linear fall-off. Matt and I played with a number of different interpolation schemes to smooth out this transition, and eventually settled on a custom smooth-step function. During this process, I made the observation that whatever blending function we used needed to introduce C1 continuity in order to remove the visual discontinuity. This observation led Brent Burley to realize that instead of a complex custom smooth-step function, a simple Hermite interpolation would be enough; this Hermite interpolation is the one presented in the talk / short paper.

For a much more in-depth view at all of the above, complete with diagrams and figures and examples, I highly recommend looking at Matt’s presentation slides and presenter notes.

Here is a test render of the Iduna character’s costume from Frozen 2, from before we had this technique implemented in Hyperion. The harsh shadow terminator produces an illusion that makes her arms and torso look boxier than the actual underlying geometry is:

Iduna's costume without our shadow terminator technique. Note how boxy the arms and torso look.

…and here is the same test render, but now with our soft shadow terminator fix implemented and enabled. Note how her arms and torso now look properly rounded, instead of boxy!

Iduna's costume with our shadow terminator technique. The arms and torso look correctly rounded now.

This technique is now enabled by default across the board in Hyperion, and any article of clothing or costume you see in Frozen 2 is using this technique. So, through this project, we got to play a small role in making Elsa, Anna, Kristoff, and everyone else look like themselves!

Hyperion Publications

July 30, 2019 | Tags: Hyperion

Every year at SIGGRAPH (and sometimes at other points in the year), members of the Hyperion team inevitably get asked if there is any publicly available information about Disney’s Hyperion Renderer. The answer is: yes, there is actually a lot of publicly available information!

Figure 1: Previews of the first page of every Hyperion-related publication from Disney Animation, Disney Research Studios, and other research partners.

One amazing aspect of working at Walt Disney Animation Studios is the huge amount of support and encouragement we get from our managers and the wider studio for publishing and sharing our work with the wider academic world and industry. As part of this sharing, the Hyperion team has had the opportunity to publish a number of papers over the years detailing various interesting techniques used in the renderer.

I think it’s very important to mention here that another one of my favorite aspects of working on the Hyperion team is the deep collaboration we get to engage in with our sister rendering team at Disney Research Studios (formerly known as Disney Research Zürich). The vast majority of the Hyperion team’s publications are joint works with Disney Research Studios, and I personally think it’s fair to say that all of Hyperion’s most interesting advanced features are just as much the result of research and work from Disney Research Studios as they are the result of our team’s own work. Without a doubt, Hyperion, and by extension, our movies, would not be what they are today without Disney Research Studios. Of course, we also collaborate closely with our sister rendering teams at Pixar Animation Studios and Industrial Light & Magic as well, and there are numerous examples where collaboration between all of these teams has advanced the state of the art in rendering for the whole industry.

So without further ado, below are all of the papers that the Hyperion team has published or worked on or had involvement with over the years, either by ourselves or with our counterparts at Disney Research Studios, Pixar, ILM, and other research groups. If you’ve ever been curious to learn more about Disney’s Hyperion Renderer, here are 50 publications with a combined 529 pages of material! For each paper, I’ll link to a preprint version, link to the official publisher’s version, and link any additional relevant resources for the paper. Please see publisher’s version or project page links for any additional supplemental materials that go with each paper. I’ll also give the citation information, give a brief description, list the teams involved, and note how the paper is relevant to Hyperion. This post is meant to be a living document; I’ll come back and update it down the line with future publications. Publications are listed in chronological order.

  1. Ptex: Per-Face Texture Mapping for Production Rendering

    Brent Burley and Dylan Lacewell. Ptex: Per-face Texture Mapping for Production Rendering. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2008), 27(4), June 2008.

    Internal project from Disney Animation. This paper describes per-face textures, a UV-free way of texture mapping. Ptex is the texturing system used in Hyperion for all non-procedural texture maps. Every Disney Animation film made using Hyperion is textured entirely with Ptex. Ptex is also available in many commercial renderers, such as Pixar’s RenderMan!

  2. Physically-Based Shading at Disney

    Brent Burley. Physically Based Shading at Disney. In ACM SIGGRAPH 2012 Course Notes: Practical Physically-Based Shading in Film and Game Production, August 2012.

    Internal project from Disney Animation. This paper describes the Disney BRDF, a physically principled shading model with a artist-friendly parameterization and layering system. The Disney BRDF is the basis of Hyperion’s entire shading system. The Disney BRDF has also gained widespread industry adoption the basis of a wide variety of physically based shading systems, and has influenced the design of shading systems in a number of other production renderers. Every Disney Animation film made using Hyperion is shaded using the Disney BSDF (an extended version of the Disney BRDF, described in a later paper).

  3. Sorted Deferred Shading for Production Path Tracing

    Christian Eisenacher, Gregory Nichols, Andrew Selle, and Brent Burley. Sorted Deferred Shading for Production Path Tracing. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2013), 32(4), June 2013.

    Internal project from Disney Animation. Won the Best Paper Award at EGSR 2013! This paper describes the sorted deferred shading architecture that is at the very core of Hyperion. Along with the previous two papers in this list, this is one of the foundational papers for Hyperion; every film rendered using Hyperion is rendered using this architecture.

  4. Residual Ratio Tracking for Estimating Attenuation in Participating Media

    Jan Novák, Andrew Selle, and Wojciech Jarosz. Residual Ratio Tracking for Estimating Attenuation in Participating Media. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2014), 33(6), November 2014.

    Joint project between Disney Research Studios and Disney Animation. This paper described a pair of new, complementary techniques for evaluating transmittance in heterogeneous volumes. These two techniques made up the core of Hyperion’s first and second generation volume rendering implementations, used from Big Hero 6 up through Moana.

  5. Visualizing Building Interiors using Virtual Windows

    Norman Moses Joseph, Brett Achorn, Sean D. Jenkins, and Hank Driskill. Visualizing Building Interiors using Virtual Windows. In ACM SIGGRAPH Asia 2014 Technical Briefs, December 2014.

    Internal project from Disney Animation. This paper describes Hyperion’s “hologram shader”, which is used for creating the appearance of parallaxed, fully shaded, detailed building interiors without adding additional geometric complexity to a scene. This technique was developed for Big Hero 6. Be sure to check out the supplemental materials on the publisher site for a cool video breakdown of the technique.

  6. Path-space Motion Estimation and Decomposition for Robust Animation Filtering

    Henning Zimmer, Fabrice Rousselle, Wenzel Jakob, Oliver Wang, David Adler, Wojciech Jarosz, Olga Sorkine-Hornung, and Alexander Sorkine-Hornung. Path-space Motion Estimation and Decomposition for Robust Animation Filtering. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2015), 34(4), June 2015.

    Joint project between Disney Research Studios, ETH Zürich, and Disney Animation. This paper describes a denoising technique suitable for animated sequences. Not directly used in Hyperion’s denoiser, but both inspired by and influential towards Hyperion’s first generation denoiser.

  7. Portal-Masked Environment Map Sampling

    Benedikt Bitterli, Jan Novák, and Wojciech Jarosz. Portal-Masked Environment Map Sampling. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2015), 34(4), June 2015.

    Joint project between Disney Research Studios and Disney Animation. This paper describes an efficient method for importance sampling environment maps. This paper was actually derived from the technique Hyperion uses for importance sampling lights with IES profiles, which has been used on all films rendered using Hyperion.

  8. A Practical and Controllable Hair and Fur Model for Production Path Tracing

    Matt Jen-Yuan Chiang, Benedikt Bitterli, Chuck Tappan, and Brent Burley. A Practical and Controllable Hair and Fur Model for Production Path Tracing. In ACM SIGGRAPH 2015 Talks, August 2015.

    Joint project between Disney Research Studios and Disney Animation. This short paper gives an overview of Hyperion’s fur and hair model, originally developed for use on Zootopia. A full paper was published later with more details. This fur/hair model is Hyperion’s fur/hair model today, used on every film beginning with Zootopia to present.

  9. Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering

    Brent Burley. Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering. In ACM SIGGRAPH 2015 Course Notes: Physically Based Shading in Theory and Practice, August 2015.

    Internal project from Disney Animation. This paper describes the full Disney BSDF (sometimes referred to in the wider industry as Disney BRDF v2) used in Hyperion, and also describes a novel subsurface scattering technique called normalized diffusion subsurface scattering. The Disney BSDF is the shading model for everything ever rendered using Hyperion, and normalized diffusion was Hyperion’s subsurface model from Big Hero 6 up through Moana. For a public open-source implementation of the Disney BSDF, check out PBRT v3’s implementation. Also, check out Pixar’s RenderMan for an implementation in a commercial renderer!

  10. Approximate Reflectance Profiles for Efficient Subsurface Scattering

    Per H Christensen and Brent Burley. Approximate Reflectance Profiles for Efficient Subsurface Scattering. Pixar Technical Memo, #15-04, August 2015.

    Joint project between Pixar and Disney Animation. This paper presents several useful parameterizations for the normalized diffusion subsurface scattering model presented in the previous paper in this list. These parameterizations are used for the normalized diffusion implementation in Pixar’s RenderMan 21 and later.

  11. Big Hero 6: Into the Portal

    David Hutchins, Olun Riley, Jesse Erickson, Alexey Stomakhin, Ralf Habel, and Michael Kaschalk. Big Hero 6: Into the Portal. In ACM SIGGRAPH 2015 Talks, August 2015.

    Internal project from Disney Animation. This short paper describes some interesting volume rendering challenges that Hyperion faced during the production of Big Hero 6’s climax sequence, set in a volumetric fractal portal world.

  12. Level-of-Detail for Production-Scale Path Tracing

    Magdalena Martinek, Christian Eisenacher, and Marc Stamminger. Level-of-Detail for Production-Scale Path Tracing. In VMV 2015: Proceedings of the 20th International Symposium on Vision, Modeling, and Visualization, October 2015.

    Joint project between Disney Animation and the University of Erlangen-Nurmberg. This paper gives an overview of a SVO-based level-of-detail system for use in production path tracing. This system was originally prototyped in an early version of Hyperion and informed the automatic shading level-of-detail system that was used on Big Hero 6; automatic shading level-of-detail has since been removed from Hyperion.

  13. A Practical and Controllable Hair and Fur Model for Production Path Tracing

    Matt Jen-Yuan Chiang, Benedikt Bitterli, Chuck Tappan, and Brent Burley. A Practical and Controllable Hair and Fur Model for Production Path Tracing. Computer Graphics Forum (Proceedings of Eurographics 2016), 35(2), May 2016.

    Joint project between Disney Research Studios and Disney Animation. This paper gives an overview of Hyperion’s fur and hair model, originally developed for use on Zootopia. This fur/hair model is Hyperion’s fur/hair model today, used on every film beginning with Zootopia to present. This paper is now also implemented in the open source PBRT v3 renderer, and also serves as the basis of the hair/fur shader in Chaos Group’s V-Ray Next renderer.

  14. Subdivision Next-Event Estimation for Path-Traced Subsurface Scattering

    David Koerner, Jan Novák, Peter Kutz, Ralf Habel, and Wojciech Jarosz. Subdivision Next-Event Estimation for Path-Traced Subsurface Scattering. In Proceedings of EGSR 2016, Experimental Ideas & Implementations, June 2016.

    Joint project between Disney Research Studios, University of Stuttgart, Dartmouth College, and Disney Animation. This paper describes a method for accelerating brute force path traced subsurface scattering; this technique was developed during early experimentation in making path traced subsurface scattering practical for production in Hyperion.

  15. Nonlinearly Weighted First-Order Regression for Denoising Monte Carlo Renderings

    Benedikt Bitterli, Fabrice Rousselle, Bochang Moon, José A. Iglesias-Guitian, David Adler, Kenny Mitchell, Wojciech Jarosz, and Jan Novák. Nonlinearly Weighted First-Order Regression for Denoising Monte Carlo Renderings. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2016), 35(4), July 2016.

    Joint project between Disney Research Studios, Edinburgh Napier University, Dartmouth College, and Disney Animation. This paper describes a high-quality, stable denoising technique based on a thorough analysis of previous technique. This technique was developed during a larger project to develop a state-of-the-art successor to Hyperion’s first generation denoiser.

  16. Practical and Controllable Subsurface Scattering for Production Path Tracing

    Matt Jen-Yuan Chiang, Peter Kutz, and Brent Burley. Practical and Controllable Subsurface Scattering for Production Path Tracing. In ACM SIGGRAPH 2016 Talks, July 2016.

    Internal project from Disney Animation. This short paper describes the novel parameterization and multi-wavelength sampling strategy used to make path traced subsurface scattering practical for production. Both of these are implemented in Hyperion’s path traced subsurface scattering system and have been in use on all shows beginning with Olaf’s Frozen Adventure to present.

  17. Efficient Rendering of Heterogeneous Polydisperse Granular Media

    Thomas Müller, Marios Papas, Markus Gross, Wojciech Jarosz, and Jan Novák. Efficient Rendering of Heterogeneous Polydisperse Granular Media. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2016), 35(6), November 2016.

    External project from Disney Research Studios, ETH Zürich, and Dartmouth College, inspired in part by production problems encountered at Disney Animation related to rendering things like sand, snow, etc. This technique uses shell transport functions to accelerate path traced rendering of massive assemblies of grains. Thomas Müller implemented an experimental version of this technique in Hyperion, along with an interesting extension for applying the shell transport theory to volume rendering.

  18. Practical Path Guiding for Efficient Light-Transport Simulation

    Thomas Müller, Markus Gross, and Jan Novák. Practical Path Guiding for Efficient Light-Transport Simulation. Computer Graphics Forum (Proceedings of Eurographics Symposium on Rendering 2017), 36(4), July 2017.

    External joint project between Disney Research Studios and ETH Zürich, inspired in part by challenges with handling complex light transport efficiently in Hyperion. Won the Best Paper Award at EGSR 2017! This paper describes a robust, unbiased technique for progressively learning complex indirect illumination in a scene during a render and intelligently guiding paths to better sample difficult indirect illumination effects. Implemented in Hyperion, along with a number of interesting improvements documented in a later paper. In use on Frozen 2 and future films.

  19. Kernel-predicting Convolutional Networks for Denoising Monte Carlo Renderings

    Steve Bako, Thijs Vogels, Brian McWilliams, Mark Meyer, Jan Novák, Alex Harvill, Pradeep Sen, Tony DeRose, and Fabrice Rousselle. Kernel-predicting Convolutional Networks for Denoising Monte Carlo Renderings. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2017), 36(4), July 2017.

    External joint project between University of California Santa Barbara, Disney Research Studios, ETH Zürich, and Pixar, with project support from Disney Animation. Developed as part of the larger effort to develop a successor to Hyperion’s first generation denoiser. This paper describes a supervised learning approach for denoising filter kernels using deep convolutional neural networks. This technique is the basis of the modern Disney-Research-developed second generation deep-learning denoiser in use by the rendering teams at Pixar and ILM, and by the Hyperion iteam at Disney Animation.

  20. Production Volume Rendering

    Julian Fong, Magnus Wrenninge, Christopher Kulla, and Ralf Habel. Production Volume Rendering. In ACM SIGGRAPH 2017 Courses, July 2017.

    Joint publication from Pixar, Sony Pictures Imageworks, and Disney Animation. This course covers volume rendering in modern path tracing renderers, from basic theory all the way to practice. The last chapter details the inner workings of Hyperion’s first and second generation transmittance estimation based volume rendering system, used from Big Hero 6 up through Moana.

  21. Spectral and Decomposition Tracking for Rendering Heterogeneous Volumes

    Peter Kutz, Ralf Habel, Yining Karl Li, and Jan Novák. Spectral and Decomposition Tracking for Rendering Heterogeneous Volumes. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2017), 36(4), July 2017.

    Joint project between Disney Research Studios and Disney Animation. This paper describes two complementary new null-collision tracking techniques: decomposition tracking and spectral tracking. The paper also introduces to computer graphics an extended integral formulation of null-collision algorithms, originally developed in the field of reactor physics. These two techniques are the basis of Hyperion’s modern third generation null-collision tracking based volume rendering system, in use beginning on Olaf’s Frozen Adventure to present.

  22. The Ocean and Water Pipeline of Disney’s Moana

    Sean Palmer, Jonathan Garcia, Sara Drakeley, Patrick Kelly, and Ralf Habel. The Ocean and Water Pipeline of Disney’s Moana. In ACM SIGGRAPH 2017 Talks, July 2017.

    Internal project from Disney Animation. This short paper describes the water pipeline developed for Moana, including the level set compositing and rendering system that was implemented in Hyperion. This system has since found additional usage on shows since Moana.

  23. Recent Advancements in Disney’s Hyperion Renderer

    Brent Burley, David Adler, Matt Jen-Yuan Chiang, Ralf Habel, Patrick Kelly, Peter Kutz, Yining Karl Li, and Daniel Teece. Recent Advancements in Disney’s Hyperion Renderer. In ACM SIGGRAPH 2017 Course Notes: Path Tracing in Production Part 1, August 2017.

    Publication from Disney Animation. This paper describes various advancements in Hyperion since Big Hero 6 up through Moana, with a particular focus towards replacing multiple scattering approximations with true, brute-force path-traced solutions for both better artist workflows and improved visual quality.

  24. Denoising with Kernel Prediction and Asymmetric Loss Functions

    Thijs Vogels, Fabrice Rousselle, Brian McWilliams, Gerhard Rothlin, Alex Harvill, David Adler, Mark Meyer, and Jan Novák. Denoising with Kernel Prediction and Asymmetric Loss Functions. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2018), 37(4), August 2017.

    Joint project between Disney Research Studios, Pixar, and Disney Animation. This paper describes a variety of improvements and extensions made to the 2017 Kernel-predicting Convolutional Networks for Denoising Monte Carlo Renderings paper; collectively, these improvements comprise the modern Disney-Research-developed second generation deep-learning denoiser in use in production at Pixar, ILM, and Disney Animation. At Disney Animation, used experimentally on Ralph Breaks the Internet and in full production beginning with Frozen 2.

  25. Plausible Iris Caustics and Limbal Arc Rendering

    Matt Jen-Yuan Chiang and Brent Burley. Plausible Iris Caustics and Limbal Arc Rendering. ACM SIGGRAPH 2018 Talks, August 2018.

    Internal project from Disney Animation. This paper describes a technique for rendering realistic, physically based eye caustics using manifold next-event estimation combined with a plausible procedural geometric eye model. This realistic eye model is implemented in Hyperion and used on all projects beginning with Encanto.

  26. The Design and Evolution of Disney’s Hyperion Renderer

    Brent Burley, David Adler, Matt Jen-Yuan Chiang, Hank Driskill, Ralf Habel, Patrick Kelly, Peter Kutz, Yining Karl Li, and Daniel Teece. The Design and Evolution of Disney’s Hyperion Renderer. ACM Transactions on Graphics, 37(3), August 2018.

    Publication from Disney Animation. This paper is a systems architecture paper for the entirety of Hyperion. The paper describes the history of Disney’s Hyperion Renderer, the internal architecture, various systems such as shading, volumes, many-light sampling, emissive geometry, path simplification, fur rendering, photon-mapped caustics, subsurface scattering, and more. The paper also describes various challenges that had to be overcome for practical production use and artistic controllability. This paper covers everything in Hyperion beginning from Big Hero 6 up through Ralph Breaks the Internet.

  27. Clouds Data Set

    Walt Disney Animation Studios. Clouds Data Set, August 2018.

    Publicly released data set for rendering research, by Disney Animation. This data set was produced by our production artists as part of the development process for Hyperion’s modern third generation null-collision tracking based volume rendering system.

  28. Moana Island Scene Data Set

    Walt Disney Animation Studios. Moana Island Scene Data Set, August 2018.

    Publicly released data set for rendering research, by Disney Animation. This data set is an actual production scene from Moana, originally rendered using Hyperion and ported to PBRT v3 for the public release. This data set gives a sense of the typical scene complexity and rendering challenges that Hyperion handles every day in production.

  29. Denoising Deep Monte Carlo Renderings

    Delio Vicini, David Adler, Jan Novák, Fabrice Rousselle, and Brent Burley. Denoising Deep Monte Carlo Renderings. Computer Graphics Forum, 38(1), February 2019.

    Joint project between Disney Research Studios and Disney Animation. This paper presents a technique for denoising deep (meaning images with multiple depth bins per pixel) renders, for use with deep-compositing workflows. This technique was developed as part of general denoising research from Disney Research Studios and the Hyperion team.

  30. The Challenges of Releasing the Moana Island Scene

    Rasmus Tamstorf and Heather Pritchett. The Challenges of Releasing the Moana Island Scene. In Proceedings of EGSR 2019, Industry Track, July 2019.

    Short paper from Disney Animation’s research department, discussing some of the challenges involved in preparing a production Hyperion scene for public release. The Hyperion team provided various support and advice to the larger studio effort to release the Moana Island Scene.

  31. Practical Path Guiding in Production

    Thomas Müller. Practical Path Guiding in Production. In ACM SIGGRAPH 2019 Course Notes: Path Guiding in Production, July 2019.

    Joint project between Disney Research Studios and Disney Animation. This paper presents a number of improvements and extensions made to Practical Path Guiding developed by in Hyperion by Thomas Müller and the Hyperion team. In use in production on Frozen 2.

  32. Machine-Learning Denoising in Feature Film Production

    Henrik Dahlberg, David Adler, and Jeremy Newlin. Machine-Learning Denoising in Feature Film Production. In ACM SIGGRAPH 2019 Talks, July 2019.

    Joint publication from Pixar, Industrial Light & Magic, and Disney Animation. Describes how the modern Disney-Research-developed second generation deep-learning denoiser was deployed into production at Pixar, ILM, and Disney Animation.

  33. Taming the Shadow Terminator

    Matt Jen-Yuan Chiang, Yining Karl Li, and Brent Burley. Taming the Shadow Terminator. In ACM SIGGRAPH 2019 Talks, August 2019.

    Internal project from Disney Animation. This short paper describes a solution to the long-standing “shadow terminator” problem associated with using shading normals. The technique in this paper is implemented in Hyperion and has been in use in production starting on Frozen 2 through present.

  34. On Histogram-Preserving Blending for Randomized Texture Tiling

    Brent Burley. On Histogram-Preserving Blending for Randomized Texture Tiling. Journal of Computer Graphics Techniques, 8(4), November 2019.

    Internal project from Disney Animation. This paper describes some modiciations to the histogram-preserving hex-tiling algorithm of Heitz and Neyret; these modifications make implementing the Heitz and Neyret technique easier and more efficient. This paper describes Hyperion’s implementation of the technique, in use in production starting on Frozen 2 through present.

  35. The Look and Lighting of “Show Yourself” in “Frozen 2”

    Amol Sathe, Lance Summers, Matt Jen-Yuan Chiang, and James Newland. The Look and Lighting of “Show Yourself” in “Frozen 2”. In ACM SIGGRAPH 2020 Talks, August 2020.

    Internal project from Disney Animation. This paper describes the process that went into achieving the final look and lighting of the “Show Yourself” sequence in Frozen 2, including a new tabulation-based approach implemented in Hyperion to maintain energy conservation in rough dielectric reflection and transmission.

  36. Practical Hash-based Owen Scrambling

    Brent Burley. Practical Hash-based Owen Scrambling. Journal of Computer Graphics Techniques, 9(4), December 2020.

    Internal project from Disney Animation. This paper describes a new version of Owen scrambling for the Sobol sequence that is both simple to implement, efficient to evaluate, and broadly applicable to various problems.

  37. Unbiased Emission and Scattering Importance Sampling For Heterogeneous Volumes

    Wei-Feng Wayne Huang, Peter Kutz, Yining Karl Li, and Matt Jen-Yuan Chiang. Unbiased Emission and Scattering Importance Sampling For Heterogeneous Volumes. In ACM SIGGRAPH 2021 Talks, August 2021.

    Internal project from Disney Animation. This paper describes a pair of new unbiased distance-sampling methods for production volume path tracing, with a specific focus on sampling emission and scattering. First used on Raya and the Last Dragon.

  38. The Atmosphere of Raya and the Last Dragon

    Marc Bryant, Ryan DeYoung, Wei-Feng Wayne Huang, Joe Longson, and Noel Villegas. The Atmosphere of Raya and the Last Dragon. In ACM SIGGRAPH 2021 Talks, August 2021.

    Internal project from Disney Animation. This paper describes the various rendering and workflow improvements that went into rendering atmospheric volumes to produce the highly atmospheric lighting in Raya and the Last Dragon.

  39. Practical Multiple-Scattering Sheen Using Linearly Transformed Cosines

    Tizian Zeltner, Brent Burley, and Matt Jen-Yuan Chiang. Practical Multiple-Scattering Sheen Using Linearly Transformed Cosines. In ACM SIGGRAPH 2022 Talks, August 2022.

    Joint project between École Polytechnique Fédérale de Lausanne (EPFL) and Disney Animation. This paper descibes the new multiple-scattering sheen model used in the Disney Principled BSDF starting with the production of Strange World.

  40. Deep Adaptive Sampling and Reconstruction Using Analytic Distributions

    Farnood Salehi, Marco Manzi, Gerhard Rothlin, Romann Weber, Christopher Schroers, and Marios Papas. Deep Adaptive Sampling and Reconstruction Using Analytic Distributions. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2022), 41(6), December 2022.

    External project from Disney Research Studios, with project support from Disney Animation. This paper extends Disney’s deep learning denoising technology to also drive adaptive sampling during the rendering process. Part of a larger joint research project between Disney Research Studios, Disney Animation, Pixar, and Industrial Light & Magic on denoising techniques.

  41. “Encanto” - Let’s Talk About Bruno’s Visions

    Corey Butler, Brent Burley, Wei-Feng Wayne Huang, Yining Karl Li, and Benjamin Huang. “Encanto” - Let’s Talk About Bruno’s Visions. In ACM SIGGRAPH 2022 Talks, August 2022.

    Internal project from Disney Animation. This paper describes the process of creating the holographic prophecy shards from Encanto, including a new teleportation shader in Hyperion that was developed specifically to support this effect.

  42. Fracture-Aware Tessellation of Subdivision Surfaces

    Brent Burley and Francisco Rodriguez. Fracture-Aware Tessellation of Subdivision Surfaces. In ACM SIGGRAPH 2022 Talks, August 2022.

    Internal project from Disney Animation. This paper describes a new tessellation algorithm for fractured subdivision surfaces, used as part of Disney Animation’s destruction FX pipeline and implemented in Hypeprion. First used in production on Encanto.

  43. Deep Compositional Denoising on Frame Sequences

    Xianyao Zhang, Gerhard Rothlin, Marco Manzi, Markus Gross, and Marios Papas. Deep Compositional Denoising on Frame Sequences. In EGSR 2023: Proceedings of the 34th Eurographics Symposium on Rendering, June 2023.

    External project from Disney Research Studios, with project support from Disney Animation. This paper unifies previously separate approaches used in Disney’s deep learning denoising system for single-frame compositional denoising and multi-frame non-compositional denoising. Part of a larger joint research project between Disney Research Studios, Disney Animation, Pixar, and Industrial Light & Magic on denoising techniques.

  44. Progressive Null-Tracking for Volumetric Rendering

    Zackary Misso, Yining Karl Li, Brent Burley, Daniel Teece, and Wojciech Jarosz. Progressive Null Tracking for Volumetric Rendering. SIGGRAPH ‘23: ACM SIGGRAPH 2023 Conference Proceedings, August 2023.

    Joint project between Dartmouth College and Disney Animation. This paper describes a new method to progressively learn bounding majorants when using null-tracking techniques to perform unbiased rendering of general heterogeneous volumes with unknown bounding majorants.

  45. Splat: Developing a ‘Strange’ Shader

    Kendall Litaker, Brent Burley, Dan Lipson, and Mason Khoo. Splat: Developing a ‘Strange’ Shader. In ACM SIGGRAPH 2023 Talks, August 2023.

    Internal project from Disney Animation. This paper describes the unusual challenges encountered when developing the unique shading and look for the Splat character from Strange World.

  46. Neural Denoising for Deep-Z Monte Carlo Renderings

    Xianyao Zhang, Gerhard Rothlin, Shilin Zhu, Tunç Ozan Aydin, Farnood Salehi, Markus Gross, Marios Papas. Neural Denoising for Deep-Z Monte Carlo Renderings. Computer Graphics Forum (Proceedings of Eurographics 2024), 43(2), April 2024.

    External joint project between Disney Research Studios and Pixar, with project support from Disney Animation. This paper describes an extension to Disney’s deep learning denoising technology to add support for deep-Z images and deep compositing workflows. Part of a larger joint research project between Disney Research Studios, Disney Animation, Pixar, and Industrial Light & Magic on denoising techniques.

  47. Cache Points for Production-Scale Occlusion-Aware Many-Lights Sampling and Volumetric Scattering

    Yining Karl Li, Charlotte Zhu, Gregory Nichols, Peter Kutz, Wei-Feng Wayne Huang, David Adler, Brent Burley, and Daniel Teece. Cache Points for Production-Scale Occlusion-Aware Many-Lights Sampling and Volumetric Scattering. In DigiPro ‘24: Proceedings of the Digital Production Symposium 2024, July 2024.

    Internal project from Disney Animation. This paper describes Hyperion’s unique many-lights importance sampling system. Used on every project rendered using Hyperion to date, this paper contains deep implementation details and notes from a decade of production experience.

  48. Dynamic Screen Space Textures for Coherent Stylization

    Brent Burley, Brian Green, and Daniel Teece. Dynamic Screen Space Textures for Coherent Stylization. In ACM SIGGRAPH 2024 Talks, July 2024.

    Internal project from Disney Animation. This paper describes a novel new dynamic screen space texturing system that makes up a key part of the stylized watercolor look of Wish.

  49. Volume Scattering Probability Guiding

    Kehan Xu, Sebastian Herholz, Marco Manzi, Marios Papas, and Markus Gross. Volume Scattering Probability Guiding. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2024), 43(6), December 2024.

    External joint project between Disney Research Studios and Intel, with project support from Disney Animation. This paper describes an improvement to volume path guiding that enables direct control over volume scattering probability. Part of a larger joint research project between Disney Research Studios, Disney Animation, Pixar, and Industrial Light & Magic on path guiding techniques.

  50. Neural Resampling with Optimized Candidate Allocation

    Alexander Rath, Marco Manzi, Farnood Salehi, Sebastian Weiss, Tiziano Portenier, Saeed Hadadan, and Marios Papas. Neural Resampling with Optimized Candidate Allocation. In EGSR 2025: Proceedings of the 36th Eurographics Symposium on Rendering, June 2025.

    Joint project between Disney Research Studios and Disney Animation. This paper presents an experimental implementation of GPU-based neural learning system inside of Hyperion’s CPU-based architecture, suitable for use as both a path guiding system and for radiance caching. Part of a larger joint research project between Disney Research Studios, Disney Animation, Pixar, and Industrial Light & Magic on path guiding techniques.

Figure 2: Hyperion logo, modeled by Disney Animation artist Chuck Tappan and rendered in Disney's Hyperion Renderer.

Again, this post is meant to be a living document; any new publications with involvement from the Hyperion team will be added here. Of course, the Hyperion team is not the only team at Disney Animation that regularly publishes; for a full list of publications from Disney Animation, see the official Disney Animation publications page. The Disney Animation Technology website is also worth keeping an eye on if you want to keep up on what our engineers and TDs are working on!

If you’re just getting started and want to learn more about rendering in general, the must-read text that every rendering engineer has on their desk or bookshelf is Physically Based Rendering 3rd Edition by Matt Pharr, Wenzel Jakob, and Greg Humphreys (now available online completely for free!). Also, the de-facto standard beginner’s text today is the Ray Tracing in One Weekend series by Peter Shirley, which provides a great, gentle, practical introduction to ray tracing, and is also available completely for free. Also take a look at Real-Time Rendering 4th Edition, Ray Tracing Gems (also available online for free), The Graphics Codex by Morgan McGuire, and Eric Haines’s Ray Tracing Resources page.

Many other amazing rendering teams at both large studios and commercial vendors also publish regularly, and I highly recommend keeping up with all of their work too! For a good starting point into exploring the wider world of production rendering, check out the ACM Transactions on Graphics Special Issue on Production Rendering, which is edited by Matt Pharr and contains extensive, detailed systems papers on Pixar’s RenderMan, Weta Digital’s Manuka, Solid Angle (Autodesk)’s Arnold, Sony Picture Imageworks’ Arnold, and of course Disney Animation’s Hyperion. A sixth paper that I would group with five above is the High Performance Graphics 2017 paper detailing the architecture of DreamWorks Animation’s MoonRay.

For even further exploration, extensive course notes are available from SIGGRAPH courses every year. Particularly good recurring courses to look at from past years are the Path Tracing in Production course (2017, 2018, 2019), the absolutely legendary Physically Based Shading course (2010, 2012, 2013, 2014, 2015, 2016, 2017), the various incarnations of a volume rendering course (2011, 2017, 2018), and now due to the dawn of ray tracing in games, Advances in Real-Time Rendering and Open Problems in Real-Time Rendering. Also, Stephen Hill typically collects links to all publicly available course notes, slides, source code, and more for SIGGRAPH each year after the conference on his blog; both his blog and the blogs listed on the sidebar of his website are essentially mandatory reading in the rendering world. Also, interesting rendering papers are always being published in journals and at conferences. The major journals to check are ACM Transactions on Graphics (TOG), Computer Graphics Forum (CGF), and the Journal of Computer Graphics Techniques (JCGT); the major academic conferences where rendering stuff appears are SIGGRAPH, SIGGRAPH Asia, EGSR (Eurographics Symposium on Rendering), HPG (High Performance Graphics), MAM (Workshop on Material Appearance Modeling), EUROGRAPHICS, and i3D (ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games); another three industry conferences where interesting stuff often appears are DigiPro, GDC (Game Developers Conference) and GTC (Graphics Technology Conference). A complete listing of the contents for all of these conferences every year, along with links to preprints, is compiled by Ke-Sen Huang.

A large number of people have contributed directly to Hyperion’s development since the beginning of the project, in a variety of capacities ranging from core developers to TDs and support staff and all the way to notable interns. In no particular order, including both present and past: Daniel Teece, Brent Burley, David Adler, Yining Karl Li, Mark Lee, Charlotte Zhu, Brian Green, Andrew Bauer, Lea Reichardt, Mackenzie Thompson, Wei-Feng Wayne Huang, Matt Jen-Yuan Chen, Joe Schutte, Andrew Gartner, Jennifer Yu, Peter Kutz, Ralf Habel, Patrick Kelly, Gregory Nichols, Andrew Selle, Christian Eisenacher, Jan Novák, Ben Spencer, Doug Lesan, Lisa Young, Tami Valdez, Andrew Fisher, Noah Kagan, Benedikt Bitterli, Thomas Müller, Tizian Zeltner, Zackary Misso, Magdalena Martinek, Mathijs Molenaar, Laura Lediav, Guillaume Loubet, David Koerner, Simon Kallweit, Gabor Liktor, Ulrich Muller, Norman Moses Joseph, Stella Cheng, Marc Cooper, Tal Lancaster, and Serge Sretschinsky. Over the years, our closest research partners at Disney Research Studios, Pixar Animation Studios, Industrial Light & Magic, and elsewhere have included (in no particular order): Marios Papas, Marco Manzi, Tiziano Portenier, Alexander Rath, Rajesh Sharma, Rasmus Tamstorf, Jan Novák, Gerhard Roethlin, Per Christensen, Julian Fong, Mark Meyer, André Mazzone, Wojciech Jarosz, Fabrice Rouselle, Christophe Hery, Ryusuke Villemin, and Magnus Wrenninge. Invaluable support from studio leadership over the years has been provided by (again, in no particular order): Nick Cannon, Munira Tayabji, Rebecca Bever, Bettina Martin, Laura Franek, Collin Larkins, Golriz Fanai, Rajesh Sharma, Chuck Tappan, Sean Jenkins, Darren Robinson, Alex Nijmeh, Hank Driskill, Kyle Odermatt, Adolph Lusinsky, Ernie Petti, Kelsey Hurley, Shweta Viswanathan, Tad Miller, Mark Hammel, Mohit Kallianpur, Brian Leach, Daniel Rice, Amol Sathe, Alessandro Jacomini, Josh Staub, Steve Goldberg, Scott Kersavage, Andy Hendrickson, Dan Candela, Ed Catmull, and many others. Of course, beyond this enormous list, there is an even more enormous list of countless artists, technical directors, production supervisors, and other technology development teams at Disney Animation who motivated Hyperion, participated in its development, and contributed to its success. If anything in this post has caught your interest, keep an eye out for open position listings on DisneyAnimation.com; maybe these lists can one day include you!

Finally, here is a list of all publicly released and announced projects to date made using Disney’s Hyperion Renderer:

Feature Films: Big Hero 6 (2014), Zootopia (2016), Moana (2016), Ralph Breaks the Internet (2018), Frozen 2 (2019), Raya and the Last Dragon (2021), Encanto (2021), Strange World (2022), Wish (2023), Moana 2 (2024), Zootopia 2 (2025)

Shorts and Featurettes: Feast (2014), Frozen Fever (2015), Inner Workings (2016), Gone Fishing (2017), Olaf’s Frozen Adventure (2017), Myth: A Frozen Tale1 (2019), Once Upon a Snowman (2020), Us Again (2021), Far From the Tree (2021), Once Upon A Studio (2023), Versa (2025)

Animated Series: At Home With Olaf (2020), Olaf Presents (2021), Baymax! (2022), Zootopia+ (2022)

Short Circuit Shorts: Exchange Student (2020), Just a Thought (2020), Jing Hua (2020), Elephant in the Room (2020), Puddles (2020), Lightning in a Bottle (2020), Zenith (2020), Drop (2020), Fetch (2020), Downtown (2020), Hair-Jitsu (2020), The Race (2020), Lucky Toupée (2020), Cycles2 (2020), A Kite’s Tale2 (2020), Going Home (2021), Crosswalk (2021), Songs to Sing in the Dark (2021), No. 2 to Kettering (2021), Reflect (2022)

Intern Shorts: Ventana (2017), Voilà (2018), Maestro (2019), June Bug (2021)

Filmmaker Co-op Shorts: Weeds (2017), Forevergreen (2025)

Disney Parks Rides3: Zootopia: Hot Pursuit (Shanghai Disneyland, 2023), Peter Pan’s Never Land Adventure (Tokyo DisneySea, 2024), Zootopia: Better Zoogether! (Disney’s Animal Kingdom, 2025)

Footnotes

1 VR project running on Unreal Engine, with shading and textures baked out of Disney’s Hyperion Renderer. keyboard_return

2 VR project running on Unity, with shading and textures baked out of Disney’s Hyperion Renderer. keyboard_return

3 CG animation provided by Disney Animation, incorporated into park rides built by Walt Disney Imagineering. keyboard_return

Nested Dielectrics

May 21, 2019 | Tags: Coding, Renderer

Table of Contents

1. Introduction
2. Problems with only Interface Tracking
3. Priority-Based Nested Dielectrics
4. References

Introduction

A few years ago, I wrote a post about attenuated transmission and what I called “deep attenuation” at the time- refraction and transmission through multiple mediums embedded inside of each other, a.k.a. what is usually called nested dielectrics. What I called “deep attenuation” in that post is, in its essence, just pure interface tracking using a stack. This post is meant as a revisit and update of that post; I’ll talk about the problems with the ad-hoc pure interface tracking technique I came up with in that previous post and discuss the proper priority-based nested dielectric technique [Schmidt and Budge 2002] that Takua uses today.

Figure 1: Ice cubes floating in tea inside of a glass teacup, rendered in Takua Renderer using priority-based nested dielectrics.

In my 2015 post, I included a diagram showing the overlapping boundaries required to model ice cubes in a drink in a glass, but I didn’t actually include a render of that scenario! In retrospect, the problems with the 2015 post would have become obvious to me more quickly if I had actually done a render like that diagram. Figure 1 shows an actual “ice cubes in a drink in a glass” scene, rendered correctly using Takua Renderer’s implementation of priority-based nested dielectrics. For comparison, Figure 2 shows what Takua produces using the approach in the 2015 post; there are a number of obvious bizarre problems! In Figure 2, the ice cubes don’t properly refract the tea behind and underneath them, and the ice cubes under the liquid surface aren’t visible at all. Also, where the surface of the tea interfaces with the glass teacup, there is a odd bright ring. Conversely, Figure 1 shows a correct liquid-glass interface without a bright ring, shows proper refraction through the ice cubes, and correctly shows the ice cubes under the liquid surface.

Figure 2: The same scene as in Figure 1, rendered using Takua's old interface tracking system. A number of bizarre physically inaccurate problems are present.

Problems with only Interface Tracking

So what exactly is wrong with using only interface tracking without priorities? First, let’s quickly summarize how my old interface tracking implementation worked. Note that here we refer to the side of a surface a ray is currently on as the incident side, and the other side of the surface as the transmit side. For each path, keep a stack of which Bsdfs the path has encountered:

  • When a ray enters a surface, push the encountered surface onto the stack.
  • When a ray exits a surface, scan the stack from the top down and pop the first instance of a surface in the stack matching the encountered surface.
  • When hitting the front side of a surface, the incident properties comes from the top of the stack (or is the empty default if the stack is empty), and the transmit properties comes from surface being intersected.
  • When hitting the back side of a surface, the incident properties comes from the surface being intersected, and the transmit properties comes from the top of the stack (or is the empty default if the stack is empty).
  • Only push/pop onto the stack when a refraction/transmission event occurs.

Next, as an example, imagine a case where which surface a ray currently in is ambiguous. A common example of this case is when two surfaces are modeled as being slightly overlapping, as is often done when modeling liquid inside of a glass since modeling perfectly coincident surfaces in CG is either extremely difficult or impossible due to floating point precision problems. Even if we could model perfectly coincident surfaces, rendering perfectly coincident surfaces without artifacts is similarly extremely difficult or impossible, also due to floating point precision problems. Figure 3 shows a diagram of how a glass containing water and ice cubes is commonly modeled; in Figure 3, the ambiguous regions are where the water surface is inside of the glass and inside of the ice cube. When a ray enters this overlapping region, it is not clear whether we should treat the ray as being inside the water or inside if the glass (or ice)!

Figure 3: A diagram of a path through a glass containing water and ice cubes, using only interface tracking without priorities.

Using the pure interface tracking algorithm from my old blog post, below is what happens at each path vertex along the path illustrated in Figure 3. In this example, we define the empty default to be air.

  1. Enter Glass.
    • Incident/transmit IOR: Air/Glass.
    • Push Glass onto stack. Stack after event: (Glass).
  2. Enter Water.
    • Incident/transmit IOR: Glass/Water.
    • Push Water onto stack. Stack after event: (Water, Glass).
  3. Exit Glass.
    • Incident/transmit IOR: Glass/Water.
    • Remove Glass from stack. Stack: (Water).
  4. Enter Ice.
    • Incident/transmit IOR: Water/Ice.
    • Push Ice onto stack. Stack: (Ice, Water).
  5. Exit Water.
    • Incident/transmit IOR: Water/Ice.
    • Remove Water from stack. Stack: (Ice).
  6. Exit Ice.
    • Incident/transmit IOR: Ice/Air.
    • Remove Ice from stack. Stack: empty.
  7. Enter Water.
    • Incident/transmit IOR: Air/Water.
    • Push Water onto stack. Stack after event: (Water).
  8. Enter Glass.
    • Incident/transmit IOR: Water/Glass.
    • Push Glass onto stack. Stack after event: (Glass, Water).
  9. Reflect off Water.
    • Incident/transmit IOR: Water/Glass.
    • No change to stack. Stack after event: (Glass, Water).
  10. Reflect off Glass.
    • Incident/transmit IOR: Glass/Glass.
    • No change to stack. Stack after event: (Glass, Water).
  11. Exit Water.
    • Incident/transmit IOR: Water/Glass.
    • Remove Water from stack. Stack after event: (Glass).
  12. Exit Glass.
    • Incident/transmit IOR: Glass/Air.
    • Remove Glass from stack. Stack after event: empty.

Observe events 3 and 5, where the same index of refraction boundary is encountered as in the previous event. These double events are where some of the weirdness in Figure 2 comes from; specifically the bright ring at the liquid-glass surface interface and the incorrect refraction through the ice cube. These double events are not actually physically meaningful; in reality, a ray could never be both inside of a glass surface and inside of a water surface simultaneously. Figure 4 shows a simplified version of the tea cup example above, without ice cubes; even then, the double event still causes a bright ring at the liquid-glass surface interface. Also note how when following the rules from my old blog post, event 10 becomes a nonsense event where the incident and transmit IOR are the same. The fix for this case is to modify the rules so that when a ray exits a surface, the transmit properties come from the first surface on the stack that isn’t the same as the incident surface, but even with this fix, the reflection at event 10 is still physically impossible.

Figure 4: Tea inside of a glass cup, rendered using Takua Renderer's old interface tracking system. Note the bright ring at the liquid-glass surface interface, produced by a physically incorrect double-refraction event.

Really what we want is to model overlapping surfaces, but then in overlapping areas, be able to specify which surface a ray should think it is actually inside of. Essentially, this functionality would make overlapping surfaces behave like boolean operators; we would be able to specify that the ice cubes in Figure 3 “cut out” a space from the water they overlap with, and the glass cut out a space from the water as well. This way, the double events never occur since rays wouldn’t see the second event in each pair of double events. One solution that immediately comes to mind is to simply consider whatever surface is at the top of the interface tracking stack as being the surface we are currently inside, but this causes an even worse problem: the order of surfaces that a ray thinks it is in becomes dependent on what surfaces a ray encounters first, which depends on the direction and location of each ray! This produces an inconsistent view of the world across different rays. Instead, a better solution is provided by priority-based nested dielectrics [Schmidt and Budge 2002].

Priority-Based Nested Dielectrics

Priority-based nested dielectrics work by assigning priority values to geometry, with the priority values determining which piece of geometry “wins” when a ray is in a region of space where multiple pieces of geometry overlap. A priority value is just a single number assigned as an attribute to a piece of geometry or to a shader; the convention established by the paper is that lower numbers indicate higher priority. The basic algorithm in [Schmidt and Budge 2002] works using an interior list, which is conceptually similar to an interface tracking stack. The interior list is exactly what it sounds like: a list of all of the surfaces that a path has entered but not exited yet. Unlike the interface tracking stack though, the interior list doesn’t necessarily have to be a stack or have any particular ordering, although implementing it as a list always sorted by priority may provide some minor practical advantages. When a ray hits a surface during traversal, the following rules apply:

  • If the surface has a higher or equal priority (so lower or equal priority number) than anything else on the interior list, the result is a true hit and a intersection has occured. Proceed with regular shading and Bsdf evaluation.
  • If the surface has a lower priority (so higher priority number) than the highest-priority value on the interior list, the result is a false hit and no intersection has occured. Ignore the intersection and continue with ray traversal.
  • If the hit is a false hit OR if the hit both is a true hit and results in a refraction/transmission event:
    • Add the surface to the interior list if the ray is entering the surface.
    • Remove the surface from the interior list if the ray is exiting the surface.
  • For a true hit the produces a reflection event, don’t add the surface to the interior list.

Note that this approach only works with surfaces that are enclosed manifolds; that is, every surface defines a finite volume. When a ray exits a surface, the surface it is exiting must already be in the interior list; if not, then the interior list can become corrupted and the renderer may start thinking that paths are in surfaces that they are not actually in (or vice verse). Also note that a ray can only ever enter into a higher-priority surface through finding a true hit, and can only enter into a lower-priority surface by exiting a higher-priority surface and removing the higher-priority surface from the interior list. At each true hit, we can figure out the properties of the incident and transmit sides by examining the interior list. If hitting the front side of a surface, before we update the interior list, the surface we just hit provides the transmit properties and the highest-priority surface on the interior list provides the incident properties. If hitting the back side of a surface, before we update the interior list, the surface we just hit provides the incident properties and the second-highest-priority surface on the interior list provides the transmit properties. Alternatively, if the interior list only contains one surface, then the transmit properties come from the empty default. Importantly, if a ray hits a surface with no priority value set, that surface should always count as a true hit. This way, we can embed non-transmissive objects inside of transmissive objects and have everything work automatically.

Figure 5 shows the same scenario as in Figure 3, but now with priority values assigned to each piece of geometry. The path depicted in Figure 5 uses the priority-based interior list; dotted lines indicate parts of a surface that produce false hits due to being embedded within a higher-priority surface:

Figure 5: The same setup as in Figure 3, but now using priority values. The path is calculated using a priority-based interior list.

The empty default air surrounding everything is defined as having an infinitely high priority value, which means a lower priority than any surface in the scene. Using the priority-based interior list, here are the events that occur at each intersection along the path in Figure 5:

  1. Enter Glass.
    • Glass priority (1) is higher than ambient air (infinite), so TRUE hit.
    • Incident/transmit IOR: Air/Glass.
    • True hit, so evaluate Bsdf and produce refraction event.
    • Interior list after event: (Glass:1). Inside surface after event: Glass.
  2. Enter Water.
    • Water priority (2) is lower than highest priority in interior list (1), so FALSE hit.
    • Incident/transmit IOR: N/A.
    • False hit, so do not evaluate Bsdf and just continue straight.
    • Interior list after event: (Glass:1, Water:2). Inside surface after event: Glass.
  3. Exit Glass.
    • Glass priority (1) is equal to the highest priority in interior list (1), so TRUE hit.
    • Incident/transmit IOR: Glass/Water.
    • True hit, so evaluate Bsdf and produce refraction event. Remove Glass from interior list.
    • Interior list after event: (Water:2). Inside surface after event: Water.
  4. Enter Ice.
    • Ice priority (0) is higher than the highest priority in interior list (2), so TRUE hit.
    • Incident/transmit IOR: Water/Ice.
    • True hit, so evaluate Bsdf and produce refraction event.
    • Interior list after event: (Water:2, Ice:0). Inside surface after event: Ice.
  5. Exit Water.
    • Ice priority (0) is higher than the highest priority in interior list (2), so TRUE hit.
    • Incident/transmit IOR: N/A.
    • False hit, so do not evaluate Bsdf and just continue straight. Remove Water from interior list.
    • Interior list after event: (Ice:0). Inside surface after event: Ice.
  6. Exit Ice.
    • Ice priority is only surface in the interior list, so TRUE hit.
    • Incident/transmit IOR: Ice/Air.
    • True hit, so evaluate Bsdf and produce refraction event. Remove Ice from interior list.
    • Interior list after event: empty. Inside surface after event: air.
  7. Enter Water.
    • Water priority (2) is higher than ambient air (infinite), so TRUE hit.
    • Incident/transmit IOR: Air/Water.
    • True hit, so evaluate Bsdf and produce refraction event.
    • Interior list after event: (Water:2). Inside surface after event: Water.
  8. Enter Glass.
    • Glass priority (1) is higher than the highest priority in interior list (2), so TRUE hit.
    • Incident/transmit IOR: Water/Glass.
    • True hit, so evaluate Bsdf and produce refraction event.
    • Interior list after event: (Water:2, Glass:1). Inside surface after event: Glass.
  9. Exit Water.
    • Water priority (2) is lower than highest priority in interior list (1), so FALSE hit.
    • Incident/transmit IOR: N/A.
    • False hit, so do not evaluate Bsdf and just continue straight.
    • Interior list after event: (Glass:1). Inside surface after event: Glass.
  10. Reflect off Glass.
    • Glass priority (1) is equal to the highest priority in interior list (1), so TRUE hit.
    • Incident/transmit IOR: Glass/Air.
    • True hit, so evaluate Bsdf and produce reflection event.
    • Interior list after event: (Glass:1). Inside surface after event: Glass.
  11. Enter Water.
    • Water priority (2) is lower than highest priority in interior list (1), so FALSE hit.
    • Incident/transmit IOR: N/A.
    • False hit, so do not evaluate Bsdf and just continue straight.
    • Interior list after event: (Glass:1, Water:2). Inside surface after event: Glass.
  12. Reflect off Glass.
    • Glass priority (1) is equal to the highest priority in interior list (1), so TRUE hit.
    • Incident/transmit IOR: Glass/Water.
    • True hit, so evaluate Bsdf and produce reflection event.
    • Interior list after event: (Glass:1, Water:2). Inside surface after event: Glass.
  13. Exit Water.
    • Water priority (2) is lower than highest priority in interior list (1), so FALSE hit.
    • Incident/transmit IOR: N/A.
    • False hit, so do not evaluate Bsdf and just continue straight.
    • Interior list after event: (Glass:1). Inside surface after event: Glass.
  14. Exit Glass.
    • Glass priority (1) is equal to the highest priority in interior list (1), so TRUE hit.
    • Incident/transmit IOR: Glass/Air.
    • True hit, so evaluate Bsdf and produce refraction event. Remove Glass from interior list.
    • Interior list after event: empty. Inside surface after event: air.

The entire above sequence of events is physically plausible, and produces no weird double-events! Using priority-based nested dielectrics, Takua generates the correct images in Figure 1 and Figure 6. Note how in Figure 6 below, the liquid appears to come right up against the glass, without any bright boundary artifacts or anything else.

For actually implementing priorty-based nested dielectrics in a ray tracing renderer, I think there are two equally plausible places in the renderer where the implementation can take place. The first and most obvious location is as part of standard light transport integration or shading system. The integrator would be in charge of checking for false hits and tracing continuation rays through false hit geometry. A second, slightly less obvious location is actually as part of ray traversal through the scene itself. Including handling of false hits in the traversal system can be more efficient than handling it in the integrator since the false hit checks could be done in the middle of a single BVH tree traversal, whereas handling false hits by firing continuation rays requires a new BVH tree traversal for each false hit encountered. Also, handling false hits in the traversal system removes some complexity from the integrator. However, the downside to handling false hits in the traversal system is that it requires plumbing all of the interior list data and logic into the traversal system, which sets up something of a weird backwards dependency between the traversal and shading/integration systems. I wound up choosing to implement priority-based nested dielectrics in the integration system in Takua, simply to avoid having to do complex, weird plumbing back into the traversal system. Takua uses priority-based nested dielectrics in all integrators, including unidirectional path tracing, BDPT, PPM, and VCM, and also uses the nested dielectrics system to handle transmittance along bidirectional connections through attenuating mediums.

Figure 6: The same tea in a glass cup scene as in Figure 4, rendered correctly using Takua's priority-based nested dielectrics implementation.

Even though the technique has “nested dielectrics” in the title, this technique is not in principle limited to only dielectrics. In Takua, I now use this technique to handle all transmissive cases, including for both dielectric surfaces and for surfaces with diffuse transmission. Also, in addition to just determining the incident and transmit IORs, Takua uses this system to also determine things like what kind of participating medium a ray is currently inside of in order to calculate attenuation. This technique appears to be more or less the industry standard today; implementations are available for at least Renderman, Arnold, Mantra, and Maxwell Render.

As a side note, during the course of this work, I also upgraded Takua’s attenuation system to use ratio tracking [Novák et al. 2014] instead of ray marching when doing volumetric lookups. This change results in an important improvement to the attenuation system: ratio tracking provides an unbiased estimate of transmittance, whereas ray marching is inherently biased due to being a quadrature-based technique.

Figures 7 and 8 show a fancier scene of liquid pouring into a glass with some ice cubes and such. This scene is the Glass of Water scene from Benedikt Bitterli’s rendering resources page [Bitterli 2016], modified with brighter lighting on a white backdrop and with red liquid. I also had to modify the scene so that the liquid overlaps the glass slightly; providing a clearer read for the liquid-glass interface is why I made the liquid red. One of the neat features of this scene are the cracks modeled inside of the ice cubes; the cracks are non-manifold geometry. To render them correctly, I applied a shader with glossy refraction to the crack geometry but did not set a priority value for them; this works correctly because the cracks, being non-manifold, don’t have a concept of inside or outside anyway, so they should not participate in any interior list considerations.

Figure 7: Cranberry juice pouring into a glass with ice cubes, rendered using Takua's priority-based nested dielectrics. The scene is from Benedikt Bitterli's rendering resources page.

Figure 8: A different camera angle of the scene from Figure 7. The scene is from Benedikt Bitterli's rendering resources page.

References

Benedikt Bitterli. 2016. Rendering Resources. Retrieved from https://benedikt-bitterli.me/resources/.

Jan Novák, Andrew Selle and Wojciech Jarosz. 2014. Residual Ratio Tracking for Estimating Attenuation in Participating Media. ACM Transactions on Graphics (Proc. of SIGGRAPH Asia) 33, 6 (Nov. 2014), Article 179.

Charles M. Schmidt and Brian Budge. 2002. Simple Nested Dielectrics in Ray Traced Images. Journal of Graphics Tools 7, 2 (Jan. 2002), 1–8.

Some Blog Update Notes

For the past few years, my blog posts covering personal work have trended towards gignormous epic articles tackling huge subjects published only once or twice a year, such as with the bidirectional mipmapping post and its promised but still unfinished part 2. Unfortunately, I’m not the fastest writer when working on huge posts, since writing those posts often involves significant learning and multiple iterations of implementation and testing on my part. Over the next few months, I’m aiming to write more posts similar to this one, covering some relatively smaller topics, so that I can get posts coming out a bit more frequently while I continue to work on several upcoming, gignormous posts on long-promised topics. Or at least, that’s the plan… we’ll see!