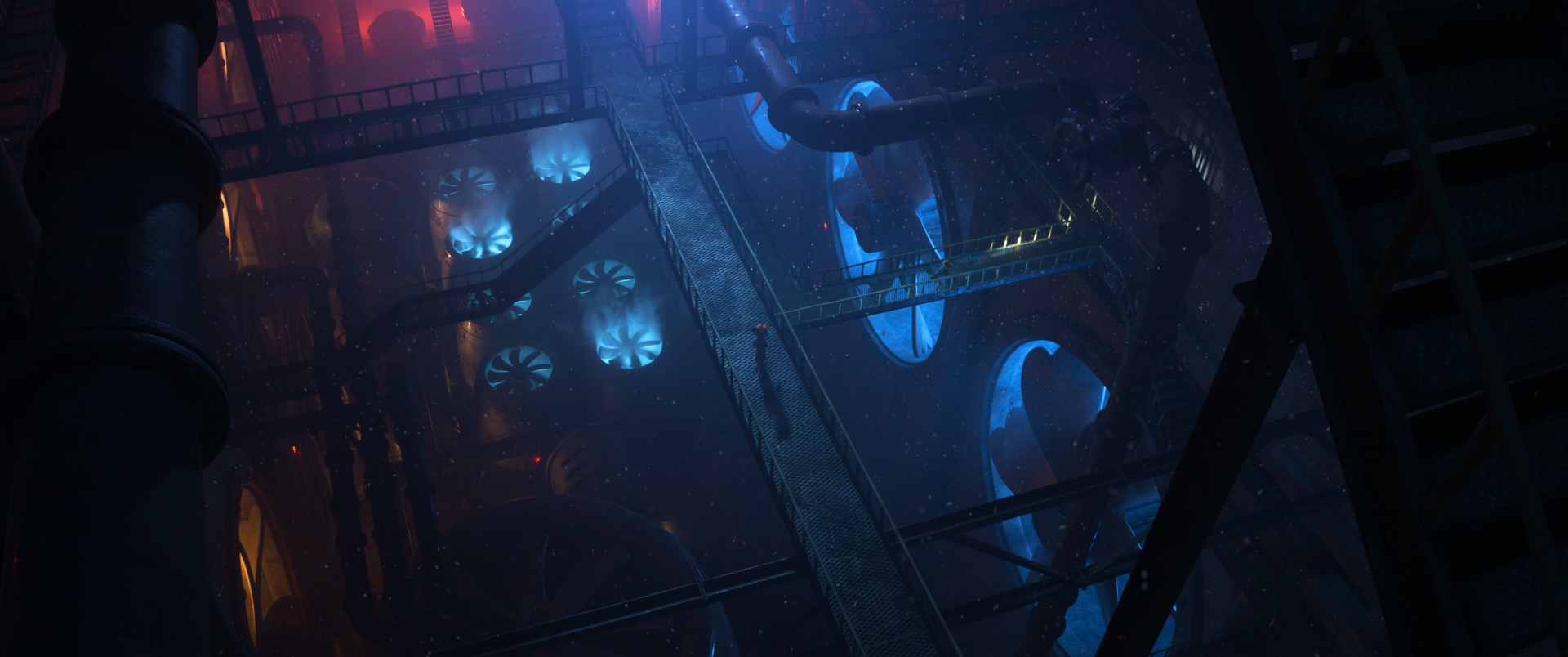Disney Animation’s movie for 2025 is Zootopia 2, which is the studio’s 64th animated feature film. Zootopia 2 picks up where the first film left off, taking us deeper into the wonderful and wild animal world of the city. One of the really fun things about Zootopia projects is that each one expands the world further. The first film introduced the setting, the Zootopia+ series on Disney+ offered fun character vignettes to expand that world, and Zootopia 2 now takes us deep into the city’s history and to places both familiar and brand new. I’ve had a great time working on Zootopia 2 for the past two years!

From a technology perspective, sequels are always interesting to work on because they give us the ability to evaluate where our filmmaking capabilities presently stand compared against a known past benchmark; we know roughly what it takes to make a Zootopia movie already, and so we can see how much better we have gotten at it in the intervening years. I think Zootopia 2 is an especially interesting case because of how important the first Zootopia (2016) was in the history of Disney Animation’s technology development. For a bit of context: the decade of Disney Animation films leading up to Zootopia (2016) was a time when the studio was rapidly climbing a steep learning curve for making CG movies. Every film had technical challenges that called for the studio to overcome unprecedented obstacles. Zootopia (2016) similarly presented an enormous list of challenges, but upon completing the film I felt there was a stronger sense of confidence in what the studio could achieve together. A small anecdote about Zootopia (2016) that I am very proud of is that at SIGGRAPH 2017, I heard from a friend at a major peer feature animation studio that they were blown away and had absolutely no idea how we had made Zootopia.

Ever since then, the sense in the studio has always been “this movie will be hard to make, but we know how to make it.” This isn’t to say that we don’t have interesting and difficult challenges to overcome in each movie we make; we always do! But, ever since Zootopia (2016)’s completion, I think we’ve been able to approach the challenges in each movie with greater confidence that we will be able to find solutions.

The major technology challenges on Zootopia 2 ultimately were pretty similar to the challenges on Zootopia (2016): everything is about detail and scale [Burkhard et al. 2016]. The world of Zootopia is incredibly detailed and visually rich, and that detail has to hold up at scales ranging from a tiny shrew to the tallest giraffe. Most characters are covered in detailed fur and hair, and because the setting is a modern city, shots can have hundreds or even thousands of characters on screen all at the same time, surrounded by all of the vehicles and lights and zillions of other props and details one expects in a city. Almost every shot in the movie has some form of complex simulation or FX work, and the nature of the story takes us through every environment and lighting scenario imaginable, all of which we have to be able to render cohesively and efficiently. Going back and rewatching Zootopia (2016), I still notice how much incredible geometry and shading detail is packed into every frame, and in the nine years since, our artists have only pushed things even further.

To give an example of the amazing amount of detail in Zootopia 2: at one point during production, our rendering team noticed some shots that had incredibly detailed snow with tons of tiny glints, so out of curiosity we opened up the shots to see how the artists had shaded the snow, and we found that they had constructed the snow out of zillions upon zillions of individual ice crystals. We were completely blown away; constructing snow this way was an idea that Disney Research had explored shortly after the first Frozen movie was made [Müller et al. 2016], but at the time it was purely a theoretical research idea, and a decade later our artists were just going ahead and actually doing it. The result in the final film looks absolutely amazing, and on top of that, instead of needing a specialized technology solution to make this approach feasible, in the past decade both our renderer and computers in general have gotten so much faster and our artists have improved their workflows so much that a brute-force solution was good enough to achieve this effect without much trouble at all.

One of the largest rendering advancements we made on Zootopia (2016) was the development of the Chiang hair shading model, which has since become the de-facto industry standard for fur/hair shading and is implemented in most major production renderers. For Zootopia 2, we kept the Chiang hair shading model [Chiang et al. 2016] as-is, but instead put a lot of effort into improving the accuracy and performance of our hair ray-geometry intersection algorithms. Making improvements to our ray-curve intersector actually took a large amount of close iteration with our Look Development artists. This may sound surprising since we didn’t change the fur shader at all, but the final look of our fur is an effect that arises from extensive multiple-scattering between fur strands, for which small energy differences that arise from inaccuracies in ray-curve intersection can multiply over many bounces into pretty significant overall look differences. In an original film, if the look of a character’s hair drifts slightly during early preproduction due to underlying renderer changes, generally these small visual changes can be tolerated and factored in as the look of the film evolves, but in a sequel with established characters that have a known target look that we must meet, we have to be a lot more careful.

I’ve been lucky enough to have gotten to work on a wide variety of types and scales of projects over the past decade at Disney Animation, and for Zootopia 2 I got to work on two of my absolute favorite types of projects. The first type of favorite project is the ones where we get to work on a custom solution for a very specific visual need in the film; these are the projects where I can point out a specific thing in final frames that is there because I wrote the code for it. My second type of favorite project is ones where we get to take something super bleeding edge from pure research and take it all the way through to practical, wide production usage. Getting to do both of these types of projects on the same film was a real treat! On Zootopia 2, working on the water tubes sequence was the first project type, and working closely with Disney Research Studios to widely deploy our next-generation path guiding system was the second project type. Hopefully we’ll have a lot more to present on both of these at SIGGRAPH/DigiPro 2026, but in the meantime here’s a quick summary.

One of the big projects I worked on for Moana 2 was a total, from-scratch rethink of our entire approach to rendering water. For the most part the same system we used on Moana 2 proved to be equally successful on Zootopia 2, but for the sequence where Nick, Judy, and Gary De’Snake zoom across the city in a water tube transport system, we had to extend the water rendering system from Moana 2 a little bit further. During this sequence, our characters are inside of glass tubes filled with water moving at something like a hundred miles per hour, with the surrounding environment visible through the tubes and whizzing by. In order to achieve the desired art direction, the tubes had to be modeled with actual water geometry inside since things like bubbles and sloshes and murk and such had to be visible, so going from inside to outside the geometry we had to render was characters inside of water inside of double-sided glass tubes set in huge complex forest and city environments. To both give artists the ability to efficiently model this setup and efficiently render these shots, we wound up building out a customized version of the standard nested dielectrics solution [Schmidt and Budge 2002]. Normally nested dielectrics is pretty straightforward to implement in a simple academic renderer (I’ve written about implementing nested dielectrics in my hobby renderer before), but implementing nested dielectrics to work correctly with the myriad of other advanced features in a production renderer while also remaining performant and robust within the context of a wavefront path tracing architecture proved to require a bit more work compared with in a toy renderer.

During Moana 2’s production, we started work with Disney Research|Studios on a next-generation path guiding system in Hyperion that supports both volumes and surfaces (unlike our previous path guiding system, which only supported surfaces); this new system is built on top of the excellent and state-of-the-art Open Path Guiding (OpenPGL) library [Herholz and Dittebrandt 2022]. Zootopia 2 is the first film where we’ve been able to deploy our next-generation path guiding on a wide scale, rendering about 12% of the entire movie using this system. We presented a lot of the technical details of this new system in our course on path guiding [Reichardt et al. 2025] at SIGGRAPH 2025, but a lot more work beyond what we presented in that course had to go into making path guiding a really production scalable renderer feature. This effort required deep collaboration between a handful of developers on the Hyperion team and a bunch of folks at Disney Research|Studios, to the point where over the past few years Disney Research|Studios has been using Hyperion essentially as one of their primary in-house research renderer platforms and Disney Research staff have been working directly with us on the same codebase. Having come from a more academic rendering background, I think this is one of the coolest things that being part of the larger Walt Disney Company enables our team and studio to do. Our next-generation path guiding system proved to be a really valuable tool on Zootopia 2; in several parts of the movie, entire sequences that we had anticipated to be extraordinarily difficult to render saw enormous efficiency and workflow improvements thanks to path guiding and wound up going through with relative ease!

One particularly fun thing about working on Zootopia 2 was that my wife, Harmony Li, was one of the movie’s Associate Technical Supervisors; this title means she was one of the leads for Zootopia 2’s TD department. Harmony being a supervisor on the show meant I got to work closely with her on a few things! She oversaw character look, simulation, technical animation, crowds, and something that Disney Animation calls “Tactics”, which is essentially optimization across the entire show ranging from pipeline and workflows all the way to render efficiency. As part of Zootopia 2’s Tactics strategy, the rendering team was folded more closely into the asset building process than in previous shows. Having huge crowds of thousands of characters on screen meant that every single individual character needed to be as optimized as possible, and to that end the rendering team helped provide guidance and best practices early in the character modeling and look development process to try to keep everything optimized while not compromising on final look. However, render optimization was only a small part of making the huge crowds in Zootopia 2 possible; various production technology teams and the TD department put enormous groundbreaking work into developing new ways to efficiently author and represent crowd rigs in USD and to interactively visualize huge crowds covered in fur inside of our 3D software packages. All of this also had to be done while, for the first time on a feature film project, Disney Animation switched from Maya to Presto for animation, and all on a movie which by necessity contains by far the greatest variety of different rig types and characters in any of our films (possible in any animated film, period). Again, more on all of this at SIGGRAPH 2026, hopefully.

I think all of the things I’ve written about in this post are just a few great examples of why I think having a dedicated in-house technology development team is so valuable to the way we make films- Disney Animation’s charter is to always be making animated films that push the limits of the art form, and making sure our films are the best looking films we can possibly make is a huge part of that goal. As an example, while Hyperion has a lot of cool features and unique technologies that are custom tailored to support Disney Animation’s needs and workflows, in my opinion the real value Hyperion brings at the end of the day is that our rendering team partners extremely closely with our artists and TDs to build exactly the tools that are needed for each of our movies, with maximum flexibility and customization since we know and develop the renderer from top to bottom. This is true of every technology team at Disney Animation, and it’s a big part of why I love working on our movies. I’ve written only about the projects I worked directly on in this post, which is a tiny subset of the whole of what went into making this movie. Making Zootopia 2 took dozens and dozens of these types of projects to achieve, and I’m so glad to have gotten to be a part of it!

On another small personal note, my wife and I had our first kid during the production of Zootopia 2, and our baby’s name is in the credits in the production babies section. What a cool tradition, and what a cool thing that our baby will forever be a part of!

Below are some beautiful frames from Zootopia 2. Every last detail in this movie was hand-crafted by hundreds of artists and TDs and engineers out of a dedication to and love for animation as an art form, and I promise this movie is worth seeing on the biggest theater screen you can find!

All images in this post are courtesy of and the property of Walt Disney Animation Studios.

References

Nicholas Burkard, Hans Keim, Brian Leach, Sean Palmer, Ernest J. Petti, and Michelle Robinson. 2016. From Armadillo to Zebra: Creating the Diverse Characters and World of Zootopia. In ACM SIGGRAPH 2016 Production Sessions. Article 24.

Matt Jen-Yuan Chiang, Benedikt Bitterli, Chuck Tappan, and Brent Burley. 2016. A Practical and Controllable Hair and Fur Model for Production Path Tracing. Computer Graphics Forum (Proc. of Eurographics) 35, 2 (May 2016), 275-283.

Sebastian Herholz and Addis Dittebrandt. 2022. Intel® Open Path Guiding Library.

Thomas Müller, Marios Papas, Markus Gross, Wojciech Jarosz, and Jan Novák. 2016. Efficient Rendering of Heterogeneous Polydisperse Granular Media. ACM Transactions on Graphics (Proc. of SIGGRAPH Asia) 35, 6 (Nov. 2016), Article 168.

Lea Reichardt, Brian Green, Yining Karl Li, and Marco Manzi. 2025. Path Guiding Surfaces and Volumes in Disney’s Hyperion Renderer- A Case Study. In ACM SIGGRAPH 2025 Course Notes: Path Guiding in Production and Recent Advancements. 30-66.

Charles M. Schmidt and Brian Budge. 2002. Simple Nested Dielectrics in Ray Traced Images. Journal of Graphics Tools 7, 2 (Jan. 2002), 1–8.

This year at SIGGRAPH 2025, Sebastian Herholz from Intel organized a followup to 2019’s Path Guiding in Production Course [Vorba et al. 2019]. This year’s edition of the course includes presentations by Sebastian on Intel’s Open Path Guiding library and on general advice for integrating path guiding techniques into a unidirectional path tracing renderer, a presentation by Martin Šik on how Chaos’s Corona Renderer uses advanced photon guiding techniques in their caustics solver, and a presentation by Lea Reichardt and Marco Manzi on the work Disney Animation and DisneyResearch|Studios have put into Hyperion’s second-generation path guiding system for surfaces and volumes. I strongly encourage checking out the whole course, but wanted to highlight Lea and Marco’s presentation in particular; they put a ton of care and effort into what I think is a really cool and unique look into what it takes to bridge cutting edge research into a production rendering environment. The course notes were written by the four presenters above, in addition to Brian Green and myself from the Hyperion development team.

The course will be presented on Tuesday August 12th, startng at 3:45 PM.

Here is the abstract:

We present our approach to implementing a second-generation path guiding system in Disney’s Hyperion Renderer, which draws upon many lessons learned from our earlier first-generation path guiding system. We start by focusing on the technical challenges associated with implementing path guiding in a wavefront style path tracer and present our novel solutions to these challenges. We will then present some powerful visualization and debugging tools that we developed along the way to both help us validate our implementation’s correctness and help us gain deeper insight into how path guiding performs in a complex production setting. Deploying path guiding in a complex production setting raises various interesting challenges that are not present in purely academic settings; we will explore what we learned from solving many of these challenges. Finally, we will look at some concrete production test results and discuss how these results inform our large scale deployment of path guiding in production. By providing a comprehensive review of what it took for us to achieve this deployment on a large scale in our production environment, we hope that we can provide useful lessons and inspiration for anyone else looking to similarly deploy path guiding in production, and also provide motivation for interesting future research directions.

The paper and related materials can be found at:

• Project Page (Author’s Version and Demo Video)
• Official Course Website
• Official Print Version (ACM Library)

All of the technical details are in the paper and presentation (and with 80 pages of course notes, of which 36 pages is the Disney Animation / DisneyResearch|Studios chapter, there are technical details for days!), so this blog post is just some personal thoughts on this project.

As mentioned in the abstract, what we’re presenting in this course is our second-generation path guiding system. Disney Animation and DisneyResearch|Studios have a long history of working on path guiding; one of landmark papers in modern path guiding was Practical Path Guiding (PPG) [Müller et al. 2017], which came out of DisneyResearch|Studios, and Hyperion was one of the first production renderers to implement PPG [Müller 2019]. We’ve used path guiding on a limited number of shots on most movies starting with Frozen 2, but as the course notes go into more detail on, for a variety of reasons our first generation path guiding system never gained widespread adoption. Several years ago, based on a research proposal drafted by Wei-Feng Wayne Huang while he was still at Disney Animation, we kicked off of a large scale project to further improve path guiding and bring it to a point where we could get widespread adoption and provide significant benefits to production. This project is a collaboration between DisneyResearch|Studios, Disney Animation, Pixar, ILM, and Sebastian Herholz from Intel; the second-generation path guiding system in Hyperion is a product of this project.

Personally, this project is one of my all-time favorite projects that I’ve gotten to be a part of, and I think this project really highlights what an incredible research organization DisneyResearch|Studios is. Getting to collaborate with rendering colleagues from across multiple labs and studios is always fun and interesting, and I think for projects like this, the huge amount of production and engineering expertise that the various Disney studios bring combined with the world-class research talent at DisneyResearch|Studios and ETH Zürich (which DisneyResearch|Studios is academically partnered with) gives unique perspectives and capabilities for tackling difficult problems. On top of the production experience from three cutting edge studios, DisneyResearch|Studios also has deep access to both source code and the engineering teams for not one but two extremely mature production rendering systems, Hyperion [Burley et al. 2018] and RenderMan [Christensen et al. 2018]; I don’t think there’s anything else quite like this setup in our industry, and I think it’s insanely cool that we get to work together like this!

One of the largest focus points for our second-generation path guiding efforts was to find a way to guide jointly for both surfaces and volumes; our first-generation PPG based system only supported surfaces. Over the past decade our artists have made heavier and heavier use of volumetrics in each successive project, to the point where now almost every shot in our movies contains some form of volumetrics, ranging from subtly atmospherics all the way to enormously complex setups like the storm battle at the end of Moana 2. We already knew from past experience that extending PPG to volumes wasn’t as easy as it might look, and a second-generation path guiding system would likely need to be a significant departure from PPG. Towards the start of this project we learned that Sebastian Herholz at Intel was working in a similar direction and had incorporated a wide swath of recent path guiding research [Müller et al. 2017, Herholz et al. 2019, Ruppert et al. 2020, Xu et al. 2024] into Intel’s open source OpenPGL library; at this point the project was expanded to include a collaboration with Sebastian. This collaboration has been extraordinarily fruitful, with work from the Disney side of things helping inform development for OpenPGL and expertise from Sebastian helping us build on top of OpenPGL.

An interesting aspect of our next-generation path guiding project is that this project has been both an academic research project and a production engineering project; over the past several years, this project has spawned a series of cool research papers, but has also included a huge effort to get all of this research implemented in Hyperion and RenderMan and into artists’ hands to actually make movies with, which means solving tons of practical production problems that sit outside of the usual research focus. On the research side, so far the project has spawned three papers. Dodik et al. [2022] improved upon PPG by using spatio-directional mixture models to improve guiding’s ability to learn and product sample arbitrarily oriented BSDFs. Xu et al. [2024] introduces a way to guide volume scattering probaiblity (which is indirectly related to distance sampling) in volume rendering, which historically has been a major missing piece in path guiding in volumes. The most recent paper, Rath et al. [2025], looks at how to incorporate GPU based neural forms of path guiding into existing CPU based renderers. Each of these research papers tackles a major challenge we’ve found while working towards making path guiding practical in production.

To bridge between the research work and building a practical production system, we’ve put a lot of work into solving both more architectural technical challenges, and more artist facing user experience challenges. One of the largest architectural technical challenges has been fitting path guiding, which learns from full path histories, into Hyperion’s wavefront rendering architecture [Eisenacher et al. 2013], in which path histories are not kept beyond the current bounce for each path (RenderMan XPU [Christensen et al. 2025] is also a wavefront system, so the challenges there are similar). Artist facing user experience challenges involve the reality that production renderers include many features that break physics to allow for better artistic control and more predictable results, which are difficult to account for when developing path guiding techniques in a purely academic renderer. Solving these engineering and user experience challenges in order to build a practical production system is the focus of our part of the course this year. What we’re presenting in the course is really a snapshot of where we were at the beginning of the year; the material in the course represents enormous progress towards a robust practical system, but this project is very much still in progress and we’ve made additional advancements since we finished writing the course materials; hopefully we can present even more next year!

My favorite part of working on these projects is always getting to work with and learn from really cool people. On the DisneyResearch|Studios side, this project has been led by Marco Manzi and Marios Papas, with significant contributions by Alexander Rath, Tiziano Portenier, and engineering support from Lento Manickathan. On the Disney Animation side, Lea Reichardt, Brian Green, and I have been working closely with Marco to build out the production system. Of course we have a long list of artists and TDs to thank on the production side for supporting and trying out this project; a full list of acknowledgements can be found on my project page and in the course notes. Pushing path guiding forward in research and production together has been the type of project where everyone on the project learns a lot from each other, the studios learn a lot and gain incredibly powerful and useful new tools, and the wider research community benefits as a whole. Investing in these types of large scale, longer term research projects is always a daunting task, and the fact that our studio leadership has given so much support this project and given us the time and resources to really make it a big success is just another testament towards the commitment Disney as a whole has towards making the best movies we can possibly make!

References

Brent Burley, David Adler, Matt Jen-Yuan Chiang, Hank Driskill, Ralf Habel, Patrick Kelly, Peter Kutz, Yining Karl Li, and Daniel Teece. 2018. The Design and Evolution of Disney’s Hyperion Renderer. ACM Transactions on Graphics. 37, 3 (2018), Article 33.

Per H. Christensen, Julian Fong, Jonathan Shade, Wayne L Wooten, Brenden Schubert, Andrew Kensler, Stephen Friedman, Charlie Kilpatrick, Cliff Ramshaw, Marc Bannister, Brenton Rayner, Jonathan Brouillat, and Max Liani. 2018. RenderMan: An Advanced Path Tracing Architecture for Movie Rendering. ACM Transactions on Graphics. 37, 3 (2018), Article 30.

Per H. Christensen, Julian Fong, Charlie Kilpatrick, Francisco Gonzalez Garcia, Srinath Ravichandran, Akshay Shah, Ethan Jaszewski, Stephen Friedman, James Burgess, Trina M. Roy, Tom Nettleship, Meghana Seshadri, and Susan Salituro, 2025. RenderMan XPU: A Hybrid CPU+GPU Renderer for Interactive and Final-Frame Rendering. Computer Graphics Forum (Proc. of High Performance Graphics) 44, 8 (Jun. 2025), Article e70218.

Ana Dodik, Marios Papas, Cengiz Öztireli, and Thomas Müller. 2022. Path Guiding Using Spatio-Directional Mixture Models. Computer Graphics Forum (Proc. of Eurographics) 41, 1 (Feb. 2022), 172-189.

Christian Eisenacher, Gregory Nichols, Andrew Selle, and Brent Burley. 2013. Sorted Deferred Shading for Production Path Tracing. Computer Graphics Forum. 32, 4 (2013), 125-132.

Sebastian Herholz, Yangyang Zhao, Oskar Elek, Derek Nowrouzezahrai, Hendrik P. A. Lensch, and Jaroslav Křivánek. 2019. Volume Path Guiding Based on Zero-Variance Random Walk Theory. ACM Transactions on Graphics (Proc. of SIGGRAPH) 38, 3 (Jun 2019), Article 25.

Thomas Müller, Markus Gross, and Jan Novák. 2017. Practical Path Guiding for Efficient Light-Transport Simulation. Computer Graphics Forum (Proc. of Eurographics Symposium on Rendering) 36, 4 (Jun. 2017), 91-100.

Thomas Müller. 2019. Practical Path Guiding in Production. In ACM SIGGRAPH 2019 Course Notes: Path Guiding in Production. 37-50.

Alexander Rath, Marco Manzi, Farnood Salehi, Sebastian Weiss, Tiziano Portenier, Saeed Hadadan, and Marios Papas. 2025. Neural Resampling with Optimized Candidate Allocation. In Proc. of Eurographics Symposium on Rendering (EGSR 2025). Article 20251181.

Lukas Ruppert, Sebastian Herholz, and Hendrik P. A. Lensch. 2020. Robust Fitting of Parallax-Aware Mixtures for Path Guiding. ACM Transactions on Graphics (Proc. of SIGGRAPH) 39, 4 (Aug 2020), Article 147.

Jiří Vorba, Johannes Hanika, Sebastian Herholz, Thomas Müller, Jaroslav Křivánek, and Alexander Keller. 2019. Path Guiding in Production. In ACM SIGGRAPH 2019 Courses. Article 18.

Kehan Xu, Sebastian Herholz, Marco Manzi, Marios Papas, and Markus Gross. 2024. Volume Scattering Probability Guiding. ACM Transactions on Graphics (Proc. of SIGGRAPH Asia) 43, 6 (Nov. 2024), Article 184.

This year at SIGGRAPH 2025, Mark Lee, Nathan Zeichner, and I have a talk about a GPU texture streaming system we’ve been working on for Disney Animation’s in-house real-time GPU ray tracing previsualization renderer. Of course, GPU texture streaming systems are not exactly something novel; pretty much every game engine and every GPU-based production renderer out there has one. However, because Disney Animation’s texturing workflow is 100% based on Ptex, our texture streaming system has to be built to support Ptex really well, and this imposes some interesting design requirements and constraints on the problem. We thought that these design choices would make for an interesting talk!

Nathan will be presenting the talk at SIGGRAPH 2025 in Vancouver as part of the “Real-Time and Mobile Techniques” session on Sunday August 10th, starting at 9am.

Here is the paper abstract:

Disney Animation makes heavy use of Ptex [Burley and Lacewell 2008] across our assets [Burley et al. 2018], which required a new texture streaming pipeline for our new real-time ray tracer. Our goal was to create a scalable system which could provide a real-time, zero-stall experience to users at all times, even as the number of Ptex files expands into the tens of thousands. We cap the maximum size of the GPU cache to a relatively small footprint, and employ a fast LRU eviction scheme when we hit the limit.

The paper and related materials can be found at:

• Project Page (Author’s Version and Demo Video)
• Official Print Version (ACM Library)

As usual, all of the technical details are in the paper and presentation, so this blog post is just my personal notes on this project.

We’ve been working on this project for a pretty long while, and what we’re presenting in this talk is actually the second generation our team has built of a GPU texture streaming system with Ptex support. The earlier first prototype of our GPU Ptex system was largely written by Joe Schutte, who we are very indebted to for paving the way and proving out various ideas, such as the use of cuckoo hashing [Erlingsson 2006] for storing keys. We learned a ton of lessons from that first prototype, which informed the modern incarnation of the system. The core of the modern system was primarily written by Mark, with a lot of additional work from Nathan to generalize the system to support both our CUDA/Optix based GPU ray tracing previsualization renderer, and our in-house fork of Hydra’s Storm rasterizer. My role on the project was pretty small; I essentially was just a consultant contributing to some ideas and brainstorming, so I’m very grateful to Mark and Nathan for having allowed me to contribute to this talk!

One of the biggest lessons I’ve learned during my professional career has been the value of building systems twice- Chapter 11 of the famous Mythical Man Month book by Frederick Brooks is all about the value of building a first version to throw away, because much of what is required to build an actually good solution can only be learned through the process of attempting to build a solution in the first place. A lot of the design choices that went into the system described in our talk draws from both the earlier prototype that was built, and also upon past experience building texture streaming systems in other renderers. For example, one big lesson that Mark and I both learned independently is that texture filtering is extremely hard (and it’s famously even harder in Ptex due to the need to filter across faces with potentially very different resolutions), and in a stochastic ray tracing renderer, a better solution is often to just point sample and lineraly interpolate between the two closest MIP levels. Mark learned this on Moonray [Lee et al. 2017], and I’ve written about learning this on the blog before. I think this project is a great example of both learning from previous attempts at the same general problem domain, but also avoiding the second-system effect; what we have today is really fast, really robust, and given how hard texture streaming generally is as a problem domain, I think Mark and Nathan did an impressive job in keeping the actual implementation compact, elegant, and easy to work with.

Of course we need to acknowledge that there have in fact been previous attempts at implementing Ptex on the GPU, with varying degrees of success. McDonald & Burley [2011] was the first demonstrated implementation of Ptex on the GPU, but required a preprocessing step and had to deal with various complications imposed by using OpenGL/DirectX hardware texturing; this early implementation also didn’t support texture streaming. Our implementation is built primarily in CUDA and bypasses all of the traditional graphics API stuff for texturing; we deal with the per-face textures at the raw memory block level, which allows us to have zero preprocessing steps and have robust fast streaming from the CPU to the GPU. Kim et al. [2011]’s solution was to pack all of the individual per-face textures into a single giant atlased texture; back when I worked on Pixar’s Optix-based preview path tracer (called RTP) this essentially was the solution that we used. However, this solution faces major problems with MIP mapping, since faces that are next to each other in the atlas but non-adjacent in the mesh topology can bleed into each other while filtering to generate each level in the MIP chain for the single giant atlas. By streaming the original per-face textures to the GPU and using exactly the same data as what’s in the CPU Ptex implementation, we avoid all of the issues with atlasing.

An interesting thing that I think our system demonstrates is that some of the preexisting assumptions about Ptex that float around in the wider industry aren’t necessarily true. For some time now there’s been an assumption that Ptex cannot be fast for incoherent access; while it is true that Hyperion gains performance advantages from coherent shading [Eisenacher et al. 2013] and therefore coherent Ptex reads, I don’t think this is really a property of Ptex itself (as hinted at by PBRT’s integration of Ptex). One notable thing about our interactive GPU path tracing use case is that the Ptex access pattern is totally incoherent for secondary bounces- we use depth-first integrators in our previz path tracer. The demo video we included with the talk doesn’t really show this since in the demo video we just show a headlight-shaded view for the sake of clearly illustrating the texture streaming behavior, but in actual production usage our texture streaming system serves multi-bounce depth-first path tracing at interactive rates without a problem.

A final note on the demo video- unfortunately I had to capture the demo video over remote desktop at the time, so there are a few frame hitches and stalls in the video. Those hitches and stalls come entirely from recording over remote desktop, not from the texture streaming system; in Nathan’s presentation, we have some better demo videos that were recorded via direct video capture off of HDMI, and in those videos there are zero frame drops or stalls even when we force-evict the entire contents of the on-GPU texture cache.

I want to thank both the Hyperion development and Interactive Visualization development teams at Disney Animation for supporting this project, and of course we thank Brent Burley and Daniel Teece for their feedback and assistance with various Ptex topics. Finally, thanks again to Mark and Nathan for being such great collaborators. I’ve had the pleasure of working closely with Mark on a number of super cool projects over the years and I’ve learned vast amounts from him. Nathan and I go back a very long way; we first met in school and we’ve been friends for around 15 years now, but this was the first time we’ve actually gotten to do a talk together, which was great fun!

That’s all of my personal notes for this talk. If this is interesting to you, please go check out the paper and catch the presentation either live at the conference or recorded afterwards!

References

Frederick P. Brooks, Jr. 1975. The Mythical Man-Month: Essays on Software Engineering, 1st ed. Addison-Wesley.

Brent Burley and Dylan Lacewell. 2008. Ptex: Per-face Texture Mapping for Production Rendering. Computer Graphics Forum (Proc. of Eurographics Symposium on Rendering) 27, 4 (Jun. 2008), 1155-1164.

Brent Burley, David Adler, Matt Jen-Yuan Chiang, Hank Driskill, Ralf Habel, Patrick Kelly, Peter Kutz, Yining Karl Li, and Daniel Teece. 2018. The Design and Evolution of Disney’s Hyperion Renderer. ACM Transactions on Graphics. 37, 3 (2018), Article 33.

Christian Eisenacher, Gregory Nichols, Andrew Selle, and Brent Burley. 2013. Sorted Deferred Shading for Production Path Tracing. Computer Graphics Forum (Proc. of Eurographics Symposium on Rendering) 32, 4 (Jul. 2013), 125-132.

Ulfar Erlingsson, Mark Manasse, and Frank Mcsherry. 2006. A Cool and Practical Alternative to Traditional Hash Tables. Microsoft Research Tech Report.

Sujeong Kim, Karl Hillesland, and Justin Hensley. 2011. A Space-efficient and Hardware-friendly Implementation of Ptex. In ACM SIGGRAPH Asia 2011 Sketches. Article 31.

Mark Lee, Brian Green, Feng Xie, and Eric Tabellion. 2017. Vectorized Production Path Tracing. In Proc. of High Performance Graphics (HPG 2017). Article 10.

John McDonald and Brent Burley. 2011. Per-Face Texture Mapping for Real-time Rendering. In ACM SIGGRAPH 2011 Talks. Article 10.